|
This article has the following sections. A Ritzian Interpretation of Variable Stars Non-pulsating Cepheid Variables Ritzian Gamma-Ray Bursts Ultra High Energy Cosmic Rays Modeling Geminga Unsung Binaries and de Sitter's Whimsical Images? GRB 790731 and omega Geminorum
A Ritzian Interpretation of Variable Stars1 - 2 - 3 - 4
An enlargement on 1987-1989 researches by V.I. Sekerin and M.S. Serbulenko Keywords: Close Binary Stars, Gamma-Ray Bursts, Pulsar Physics, Variable Speed of Light
|
|
Preface[Added 21 Aug 2018.]In 1968 I was involved in a Naval data communications evaluation project. In my off-duty hours I was doing some experiments leading to what could be called aeroelectric propulsion. One day, at work, I brought my experiments to the attention of Lester J. Kinkel, a radio communications engineer. (He was our "Go To" guy/guru) on the Navy project. My first sentence was, "Want to know how to build a flying saucer?" He nodded, "Yes." My second sentence was, "What you do, is impress a high voltage on sharp points along the leading edge of a non-conductive airfoil ..." At that point he interrupted, "Hold it!.. Hold it!" . . . "I'll hear you out, but you need to know that you just violated one of the principles of my religion. ... You mentioned high voltage and sharp points in the same breath." (High voltages on sharp points cause corona discharges which produce radio noise that can obscure weak incoming radio signals. Lester and his like-minded engineers were in the business of doing all within their power to eliminate sharp points on high voltage surfaces.) Lester did hear me out and I seem to recall that he contributed at least one helpful pointer. Later that day it dawned on me that radio communications engineers who remain true to the above mentioned religious pragmatic imperative will not likely experience the joy of building aero-electric propulsion aircraft. For myself, I was already an apostate in physics, but even so, in 1972 I was granted a US Patent based loosely on my experiments. My patent attorney, who had formerly been the patent counsel for the Naval Electronics Laboratory Center in San Diego, confided that something seemed odd about the number of existing patents in our area of concern. (There were very few patents.) He said that the paucity of existing patents would normally be taken as evidence that the area was brand new (which he doubted) or on the other hand, there might be a lot of classified patents which we would not be able to access. (I decided to not mention flying saucers in my claim.)
I harbor the opinion that, as long as astrophysicsts religiously adhere to the pragmatic imperative of Einstein's second postulate of relativity, they will not get to experience the joy of understanding so-called radially pulsating stars (Cepheids for example) and what are thought to be explosive stars (all the way from novae and super novae to gamma-ray bursts and gamma-ray repeaters). |
|
This article is written under the presumption that the constancy of the "measured" speed of light by all observers (in vacuo) is an unresolved issue. The author favors Ritz's use of c+v relativity but with the reservation that extinction (Tolman or Ewald-Oseen), i.e., the speed of light eventually reaches a terminal speed with respect to any given medium, has to be taken into account. De Sitter's (1913) argument against Ritz is used as a theoretical springboard from which to examine currently published observations of what are thought to be radially pulsating variable stars. High-angular-resolution photographs of these variables obtained from the Hubble Space Telescope (HST), the very large array (VLA) radio telescope(s), the growing family of very large telescopes (VLTs), and/or the publication of light curves along with phase-matched spectroscopic line profiles (absorption and emission) can be used to resolve the c+v question.
|

|
In 1908 Walter Ritz formulated an emission theory of general electrodynamics(1).
in which the velocity of a light source is vectorially additive to the velocity
of the light emitted by it, i.e., the velocity of light is c + v. That aspect
of Ritz's theory does not hold for macroscopic-scale paths in dispersive media such as
the earth's atmosphere. Ritz was aware of the problem, and intended to revise his
theory, but he died in 1909 and didn't get to do the revision. The theory, as it
stands, may still find application on intermolecular and atomic scales and for modest
distances in highly rarefied regions in the interstellar medium. This article deals
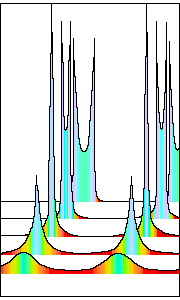
primarily with the latter case. For example, the light curves in the figure to the
left were produced by a computer program which simulates the orbit of one component
of a spectroscopic binary. (The color gradations were added manually.) The program
uses c + v relativity to calculate the light travel time to various extinction
distances. The vectorial addition of the star's instantaneous orbital velocity with that
of light (in the direction of the observer) produces arrival-time modulation, which
leads to "observed" intensity and color modulation. |
|
In 1913 Willem de Sitter urged abandonment of the Ritz theory because binary stars failed to show the predicted c + v effects(2). De Sitter's binary star argument was along the following lines. The addition of the velocity of a visible component of a binary star to the velocity of its light emitted in the direction of an observer would allow slower light (c - v) from one side of the orbit (when the component was traveling away from the observer) to be overtaken by the faster light (c + v) from one half orbit later (when the component was traveling toward the observer). At the right distance this effect could cause the visible component to periodically be seen at two different locations simultaneously and generally would lead to apparent observational departures from Keplerian motion. (The expression to compute the overtaking distance, which is a function of orbit period and orbital speed, is derived below.) Actually de Sitter focused mainly on spectroscopically double stars (with parallaxes on the order of 0.1 arc sec and less) and with the idea that their conformance with Keplerian motion (based on radial velocity measurements alone) was to be taken as evidence against the Ritz theory. See: Binary Stars as Evidence against Ritz's Relativity. [Added 15 May 2004. Updated 14 Dec 2009.]
Ritz had already alluded to this kind of possibility. In his 1908 paper he said: "I would like to remark that if P' is animated by an oscillatory movement and if the distance PP' is sufficiently large, it is possible that the waves starting at moments t'(1), t'(2), ... where the speed of P' had different values v'(1), v'(2), ..., will arrive at P simultaneously because of the difference of their speed of propagation. In practice this case will be presented only in Optics." (W. Ritz, Ann. Chim. Phys., 13, 145 (1908): pp. 213-214.)
Contrary to the de Sitter claim, and to other arguments advanced more
recently, John Fox(3) found that visible binary stars do not offer
evidence against the Ritz theory. He takes this stand on the basis of
Tolman's extinction theorem (3a)(*), i.e., the absorption and re-radiation
of electromagnetic radiation by electrical charges in a dispersive medium
leads to a terminal speed for light with respect to the medium.
The Ewald-Oseen extinction theorems (3b) are related to this idea.
Fox states that one extinction length in our local interstellar medium,
is estimated to be on the order of one light year. His laboratory tests,
however, suggest that extinction distances may be much shorter than our
current estimates. (Reference to be added.)
In the binary star case, bound atomic charges in the interstellar
environment within a light year or less of the binary star absorb and
re-emit the light from each visible component, so that beyond five extinction
lengths the re-emitted light travels at the speed of light with respect to
the bulk motion of the interstellar medium. (*) Fox attributed this action to Richard Tolman, but Tolman strictly dealt with an abrupt change from c to -c, during light's perpendicular reflection from a mirror. Tolman and de Sitter seem to have thought that interstellar gas, as well as the Earth's atmosphere, had no effect on the speed of light. [This correction was added on 27 Jul 2004. Tweaked on 07 Mar 2006.] In 1987 Vladimir Sekerin of Novosibirsk, Siberia, in an article titled Gnosiological Peculiarities in the Interpretations of Observations (For Example the Observation of Binary Stars)(4), showed that when we consider the distances (binary-to-observer) required for de Sitter's "whimsical" images effect to manifest themselves that the angular resolution of our best telescopes (1987) are insufficient for us to resolve them. An English translation of Sekerin's paper is on this website. Sekerin does not address extinction effects but he claims that de Sitter's hypothetical c + v binary star scenario provides an alternate explanation for the periodic light and apparent radial velocity variations of periodic variable stars which he says are really spectroscopic binaries. Because these images can't be resolved we won't see a visible component at two locations simultaneously, rather, we will get periodic variations in light intensity and color. The following derivation shows how to compute the distance necessary for the faster light to exactly overtake the slower light of one half orbital period earlier. We set the time interval (t1) required for the slower light (visible component receding from observer) to reach the observer at distance (L), to be:
and time interval (t2) which is the sum of the time for one half orbit (T) plus the time for the faster light (component approaching observer) to travel the same distance L:
For t1 = t2 we have:
Re-arranging and solving for L we get:
In the following text and figures Lo will represent the exact overtaking distance in the derivation above and L will represent the observer's fraction of or multiple of the distance Lo from the binary.
|
Contact Robert Fritzius at
fritzius@bellsouth.net
Top