An Astronomical Proof for the Constancy of the Speed of Light By W. de Sitter Translated from Physik. Zeitschr. 14, 429, (1913) German | Scanned | English Trans     When a source of light has a speed of u, say in the direction of the positive X axis -- according to the theory of Ritz the speed of the light emitted in the same direction is c + u, where c is the speed of light emitted by a resting source. In other theories (Lorentz, Einstein) the speed of light is always constant, equal to c, independent of the movement of the source. Now it is to be seen, that Ritz's accepted dependence of the speed of light on the movement of the source is absolutely inadmissible.     One imagines a binary star, and an observer at a great distance Δ in the plane. 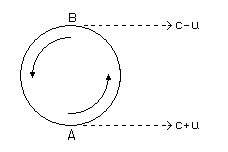Light emitted by the star from points near A (see figure) becomes observed, in accordance with the theory of Ritz, after a time Δ/(c+u), that light emitted from B after the time Δ/(c-u). We call T the half orbit time of the star (its path, for the sake of simplicity, is considered to be a circle), so the time interval between the two observations is     T + 2u Δ/c2[* - See diagram at end]. If the star goes in the second half of its period from B to A, then the observed time interval is T-2u Δ/c2. In the customary theory both intervals are equal to T. Now if 2u Δ/c2 is on the same order of magnitude as T, then if the Ritz theory were true, it would be impossible to bring the observations into agreement with Keplerian laws. With all spectroscopic binary stars 2u Δ/c2 is now indeed not only of the same order of magnitude as T, but probably in most cases even much larger. One takes e.g. u=100 km/sec, T = 8 days, Δ/c = 33 years (i.e. a parallax of 0.1"), then one has approximately T-2u Δ/c2 = 0. All these dimensions are on an order with the best known spectroscopic binary stars. (Most parallaxes will probably be smaller than 0.1".)     The existence of spectroscopic binary stars and the circumstance, that... in most cases the observed radial velocity completely becomes represented by the Keplerian motion is thus a strong proof for the constancy of the speed of light. One may still be reminded, that in many cases the radial velocities of derived orbits are corrborated by visual observations (as with δ Equulei, ζ Herculis, etc.) or by the observation of the darkening of one component of a binary star by the other (as with Algol-variables).     Leiden, February 1913.                                                             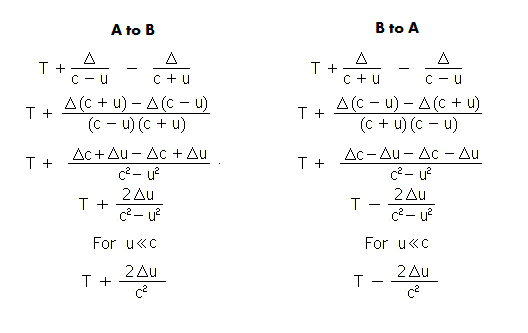(Received 14 February 1913) __________ [*] Derivation of Delay Expressions Installed on 15 May 2004. Latest update 21 Jul 2011. Thanks to ADAM 27 for translation improvement. Shade Tree Physics