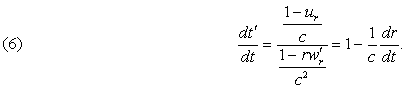Home | Up One Level | Previous | Next
Table of Contents | Previous Section | Next Section
SECOND PART
§ 1. -- GENERAL CONSIDERATIONS, PROPAGATION OF FORCES
WALTER
RITZ
Translated from Recherches
critiques sur l'Électrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.
Annales
209 (Oeuvres 370)
In this second part I intend to study the formulae of
elementary actions, to which, as we have seen, is reduced in last analysis to
Lorentz's mathematical theory, and to show that we can eliminate absolute
motion and that we can generalize it considerably without ceasing to be in
agreement with experiment. I will take up, with no change, the physical
hypotheses: the nature of electricity, the current of conduction, dielectrics,
etc., and especially the principle of superposition, which states the complete
independence of effects of diverse charges which comprise a system.¹
For this, I will be compelled to offer for the propagation
of electrodynamic actions a new image, but as it has been said in the
introduction, I will not draw all the consequences, in offering here only the
work of a critic.
A first consequence of the principle of relativity is
immediate. In the theory of ether, a material point P, at rest in (Oeuvres 371)
relation to its surroundings, will be able to emit waves of a constant radial
speed and which will make at each instant a system of spheres having P as a
center. If P
¹Because of the movements of the pure ether,
which in principle is not rigorously seen in the theory of Hertz, and there are
certain reservations that have to be made on this subject.
is animated by a motion of translation, the spheres, on the contrary, will
become eccentric, each keeping its center at P1 of ether which coincides with P
at the instant of emission. According to the principle of relativity, on the
contrary, if the motion of translation is uniform, the spheres will have to
stay concentric, as at rest, and the center will always be P. When the motion
is no longer uniform, the principle will no longer be sufficient to determine
the movement of the waves.
There are two ways to represent the phenomena. Two
distinct images have successfully ruled in Optics: the one of emission (the
light moves) and the one of ether (the light is propagated)¹ The second one
introduces absolute motion while the first leads to the movement of light in
vacuum exactly as the law that requires the principle of relativity: the
luminous particles expelled in all directions at instant t move with a constant radial speed and form a sphere for which the
center is animated with the motion of translation w that had P at the instant of emission. If w is
constant, this center will continue therefore to coincide with P.
[See the Light Motion animations.]
It is this fundamental image only that we will borrow from
the theory of emission. Needless to add that these particles must be considered
uniquely as a fiction, furthermore convenient, and which has the advantage of
¹ According to the sensible signs by which we define the identity of one part of a
continuous body with itself during movement, this will be known as "real
movement" or "movement of propagation." These sensible signs
being missing for light, we don't see any actual difference in direction
between these statements; "the light is projected" and "the
light is propagated." There is only one difference in language, or, which
comes back to the same, a difference in the sensible image that we evoke to
give an account for our sensations. The consequences which we draw from these
images are the only difference, and it is their simplicity which determines the
choice.
leading us, as we have just seen, to state for the velocity of light in a
vacuum a precise law, even when the speed P is variable and the principle of
relativity isn't sufficient. The velocity of light then depends on that
possessed by the body that emits it at the instant of emission. From that
instant, the velocity of the particles remains invariable, whatever (Oeuvres
372) the subsequent motion of P is, even
when the particles pass through ponderable bodies or electric charges. I
said in the introduction that this hypothesis, which is required by the
superposition principle, is only temporary and is contrary to that of action
and reaction, but the advantage of being as close as possible to the corresponding
hypotheses of Lorentz makes it preferable for the goal I intend here.
We will admit furthermore that the action of P on a body
P' will depend only on the velocity, the disposition, etc., of particles
emitted by P and having reached P' at the instant considered.
We could try to explain the phenomena by the mechanical
actions exerted by these particles, but the difficulties to which we are led in
doing so seem to be insurmountable. Instead of seeking to conserve the schema
of classical mechanics with "invisible masses" or
"liaisons," etc., I preferred to reduce, as much as possible, the
number of hypotheses, a method, which from the point of view of logic and
clarity, has the advantage to compensate that of Maxwell's "mechanical
analogies." We will see, by the way, that mechanical mass can be deduced,
as in Lorentz's theory, from purely electrical actions, and that besides this,
the theory is applicable to gravitation and perhaps to molecular motions. It
would encompass classical mechanics and make kinetic and potential originate
from the same
source. Under these conditions it is more satisfying, from a logical point
of view, to make use in the fundamental hypotheses only kinetic considerations,
allowing only notions of time, space and electric charge.
I will admit therefore that any electrified point emits at
each instant and in all directions fictitious particles, infinitely small,
animated by the same radial speed c
at the origin and conserving their uniform motion, no matter what bodies they
meet¹; the ensemble of particles emitted at instant t' by a (Oeuvres 373) mobile point P' at coordinates x',y'z', functions of t' will form at each subsequent instant t a sphere of radius
The center of the sphere, which continues to move with a velocity v' = v'(t') that was P' at instant t' has for coordinates
The equation for the sphere will therefore be
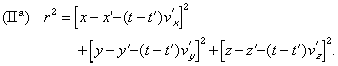
If x',y',z' are known functions of t', we will deduce from these two equations the instant of emission t' of a wave which reaches a given point P, of coordinates x,y,z at the instant t, or, which according to I, amounts to the same, the radius r of the sphere it forms at the instant and which is
¹ The modern theory of
dispersion and Lorentz's theory have this same hypothesis; the change of the
speed of light in different media appears then as the result of interference
and complex resonance phenomena.
given by
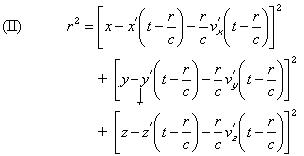
In Lorentz's theory, and in choosing a system of fixed coordinates in relation to the ether, we would have, on the contrary, the following equations:
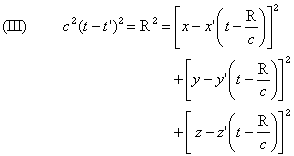
The new hypothesis introduces a complete symmetry when the two points P, P' are each animated by a uniform speed: r in this case will be the real distance between the points at the instant t. Two waves emitted simultaneously by P' and P will arrive (Oeuvres 374) simultaneously at P and P'. It isn't so in Lorentz's theory, and the consequence will be that in the case of a measurably uniform movement, where radiation is consequently nil, our theory will lead to the equality of action and reaction, which isn't the case in Lorentz's theory. It is only when there is no longer this identity of instants of emission that this principle will have to be modified, which besides is easily conceived.
Let's observe again that, if P' is animated of an
oscillatory movement and if the distance PP' is sufficiently large, it will be
possible that waves started in instants 
where the speed P' had different values 
arrive simultaneously at P as a consequence
of the difference of their speeds of propagation; in practice this case will be presented only in optics. In Lorentz's theory P' must take at certain instants a superior speed than that of light so that an analogous phenomenon is produced.
If 
are the
accelerations of points xyz, x'y'z',
and if moreover
are the components of the relative speed of the point P(x,y,z) and the
center C of the sphere emitted by P' and reaching P at t: if the motion of P' is uniform, it will be simply the relative
speed of P and P'.
The vector r, of
which the components are
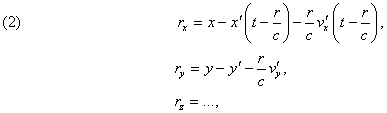
is, as we have seen, the line joining P' to P, where P' would be if its speed had remained constant in magnitude and direction since the instant of emission
(Oeuvres 375) this vector is directed from P' to P and we have
The relative velocity U of particles emitted by P', in relation to P, has for components
its square is
its projection on r is
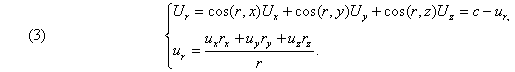
The relative position and motion of the sphere and of the point P are in fact determined when we take r, ur and u2 or, and this is the same, r, Ur, and U2; there is no combination of vectors r, u, independent from the absolute position in the space, which could not be expressed by these three quantities.
We can notice also that, for an observer placed in P and participating in the movement of this point, the ratio of the normal distance of two successive positions of the sphere, divided by the time dt, which corresponds to the speed of propagation of the wave for this observer, is precisely Ur.
Finally, if we admit that the number of
particles emitted by a charged center during a period dt' is proportional to its charge e' and to dt', the number
of particles located in an element of surface dS of the sphere will be independent of the position of this
element and proportional to
. If two spheres emitted at t' and t'+dt' are at the
normal distance dn at the point xyz at the instant t, we will have
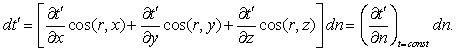
(Oeuvres
376) The number of particles
in the element of volume dSdn is then
proportional to 
, and the density D
is 
, where ca
means the universal factor of proportionality. Since r=c(t-t'),
we finally have therefore
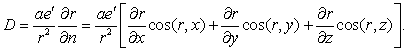
The equation (II) defines r as implicit function of the variables x, y, z, t when the motion of P' is given. We have, differentiating it,
from whence
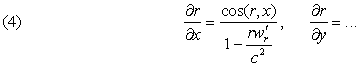
so that it comes to
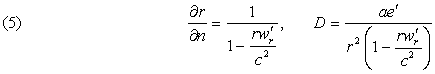
and, likewise, to terms of the nearest superior order,
The derivatives of r, D with respect to x, y, z introduces therefore the accelerations.
Considering x, y, z as functions of t, the formula should be noted
