Ritz's 1908 emission theory grand synthesis(1), held that, contrary to the Second Postulate of Special Relativity, the velocity of light sources are additive to the velocity of light. This emission theory (with one modification) appears capable of explaining some of the oddities of many types of what are thought to be intrinsically variable stars. For appropriately located observers, Ritz's relativity leads to arrival-time modulation of the light from individual components of closely interacting binary and multiple star systems. Computer code that models this Ritzian Relativity effect can produce light curves and line profiles consistent with pulsating or eruptive single stars. Ultimately the theory leads to an new explanation for the central engines of Gamma-Ray Bursts.

- - - - - - -

According to Robert Shankland(2), Einstein said that in the years prior to 1905 he had considered using an emission theory similar to that of Ritz. Einstein told Shankland that he gave up that approach because he could think of no form of differential equation that could have solutions representing waves whose velocity depended on the motion of the source. In that case the variable speed of light of the emission theory would lead to phase relations such that propagated light would be all badly "mixed up" and might even "back up on itself."

Even though Ritz accepted the mixed up light problem as part of the way things are, the c + v aspect his theory, was not applicable to light traveling over macroscopic length paths through gaseous media, such as the Earth's atmosphere. Light speed in the dispersive media is determined by a combination of the speed of light in vacuum and the index of refraction of the given medium. Ritz was fully cognizant of this fact and he planned to revise his theory. However, he died in 1909 and his work remains unfinished.

In 1913 Willem de Sitter, who was an ardent supporter of the special theory of relativity, presented two papers(3)(4) and wrote two articles(5)(6) in which he attempted to bury the competition, i.e., Ritz's emission theory He used the apparent motion of spectroscopic double stars as his shovel.

His binary star argument was, in part, along the following lines.

The addition of the velocity of a visible component of a binary star to the velocity of its light emitted in the direction of an observer would allow slower light (c - v) from one side of the orbit to be overtaken by the faster light (c + v) from one half orbit later. At a certain distance this effect could cause the visible component to periodically be seen at two different locations simultaneously and generally would lead to apparent observational departures from Keplerian motion.

De Sitter's expression to compute the distance required for the faster-later light to catch up with the slower-earlier light, is derived from the following relation. (This is not exactly de Sitter's derivation, but it is equivalent.)

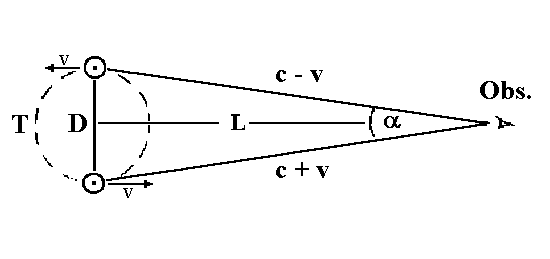
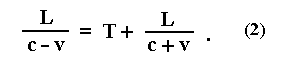
Re-arranging and solving for L we get:

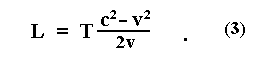
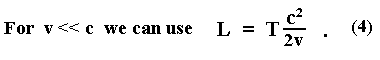
In 1965 John Fox(7) proposed the following modification to Ritz's theory to bring it into harmony with sources moving with respect to dispersive media such as the Earth's atmosphere.

"When a light wave sets into motion the charges of a medium; these in turn emit new waves whose centers move in vacuum [in between absorption / emission events] with the velocity of the charges of the medium." By this means, whatever speed the light posessed before entering the medium, it would eventually come to be traveling at the speed of light for that medium. (Fox attributed this action to Richard Tolman(8), but Tolman strictly dealt with an abrupt change to c during reflection from a mirror. Tolman and de Sitter seem to have thought that interstellar gas, as well as the Earth's atmosphere, had no [significant] effect on the speed of light. (Refs as above.)

The effect is supposed to be exponential. Five extinction lengths would be required to make the process essentially 100 percent complete.

Fox calculates one extinction length in Earth's sea-level atmosphere to be on the order of 0.3mm. (7, p. 5). Based on an estimated galactic spiral arm interstellar gas density of one hydrogen atom per cubic centimeter, he calculates an extinction distance (for visible light) to be on the order of one light year(7, p. 6).

Fox says that de Sitter failed to take extinction into consideration, and that the common atmospheres thought to surround most binary stars would tend to extinguish the evidence of light traveling either faster or slower than c(7, p. 5). He also raises a related issue. "For example, on the Ritz theory the light from a high-velocity, short period binary with insufficient atmosphere for complete extinction might bring us some evidence of its nonconstant velocity even though it is extinguished after about one light year. If no such evidence can be found, that would be support for the assumption of special relativity."(7, p. 6)

Fox concludes that the majority of tests done to decide between Ritz and Einstein, regarding the merits of the second postulate, have been invalid because of extinction.

In 1987, Vladimir Sekerin(9), who also does not address extinction effects, postulated that de Sitter's binary star scenario provides a possible explanation for the magnitude and apparent radial velocity variations of periodic variable stars, which he says may actually be spectroscopic binaries.

---

Sekerin is not the first person to have proposed apparent stellar magnitude variability based on Ritzian c+v effects. See the postscript at the end of this web page. [Added 04 November 2004.]

---

In the following text and figures L will represent the exact overtaking distance in de Sitter's derivation above and Lo will represent the observer's fraction of (or multiple of) the distance L from the binary (or multiple) system.

Sekerin's colleague, M.S. Serbulenko, furnished the following three computer generated images, depicting brightness and apparent velocity curves, produced in accordance with Sekerin's binary star scenario. Figures 1, 2 and 3 are scanned-in copies of Serbulenko's photographs. These plots are for a binary system with one visible component.

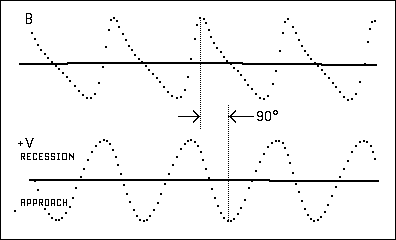
Figure 1. Brightness and Apparent Radial Velocity for
Lo = 0.07 L.

Figure 1, according to Sekerin, could be for a Cepheid variable. However, for Cepheids, the peak (approaching) apparent radial velocity curve coincides with the peak of the brightness curve. Sekerin's radial velocity curve lags his brightness curve by 90 degrees.

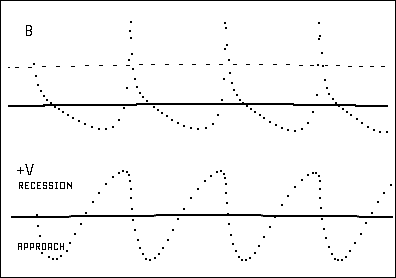
Figure 2. Brightness and Apparent Radial Velocity for
Lo = 0.72 L

The magnitude spikes in Figure 2 would appear to be very energetic.

In Figure 3 we have later emitted light periodically arriving at the observer before earlier emitted light, we get "Arrival-Time Modulation." or as Einstein said, "Badly mixed up."

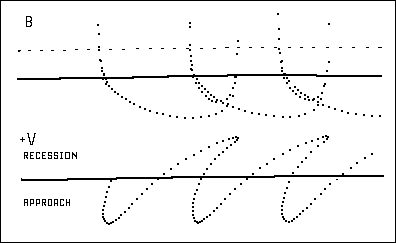
Figure 3. Brightness and Apparent Radial Velocity for
Lo = 2.8 L

The author wrote computer code that also simulates Sekerin's binary star scenario. It, like Sekerin's model, revealed a 90 degree phasing error between the magnitude and radial velocity curves. Sekerin had strictly been using Doppler effects to calculate radial velocity variations. The problem was fixed by replacing the Doppler calculations with the following expression..

fo = fs / (d Tau / dt),

where fo represents the observed frequency, fs is the raw (unshifted) source frequency, and dTau/dt represents the differential of observed arrival-times versus real-time. (Up close to the binary, this expression behaves like a Doppler calculation.)

Figures 4 and 5 show a comparison of Doppler versus time-modulation induced apparent radial velocity effects. Note that the Doppler version has the same 90 degree phase error as produced by Serbulenko's computations as seen in Figure 1.

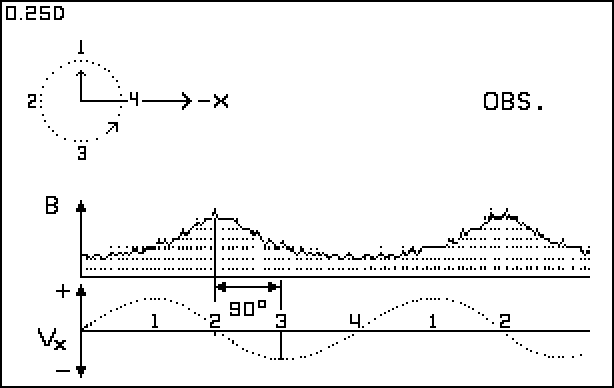
Figure 4. Lo = 0.25 L - Doppler

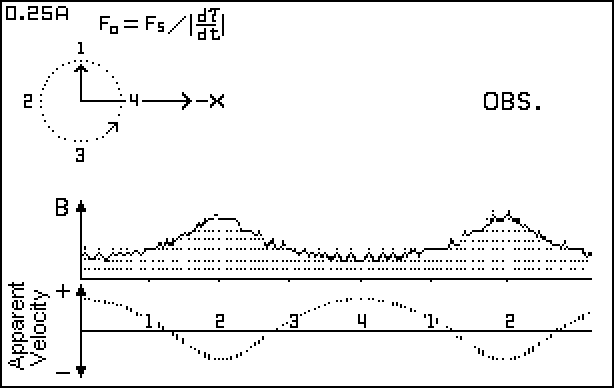
Figure 5. Lo = 0.25 L - Time Modulation

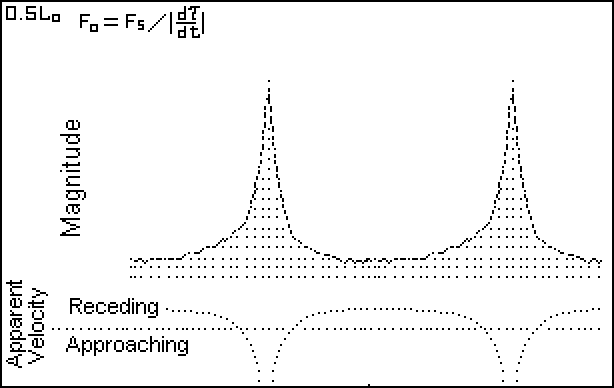
Figure 6. Lo = 0.5 L - Time Modulation

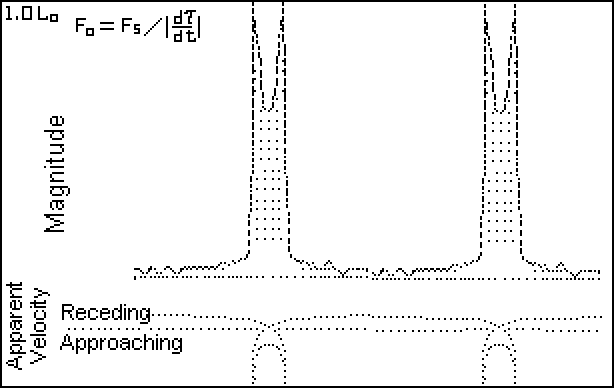
Figure 7. Lo = 1.0 L - Time Modulation

When d Tau / dt approaches zero, the apparent radial velocity approaches infinity. The infinite peaks do not match any intrinsic stellar physical process. (Physical objects simply do not attain infinite speeds of expansion or contraction.) The velocity curve shows line-doubling in the saddle region which is caused by the radial velocity information looping back (time-wise) on itself.

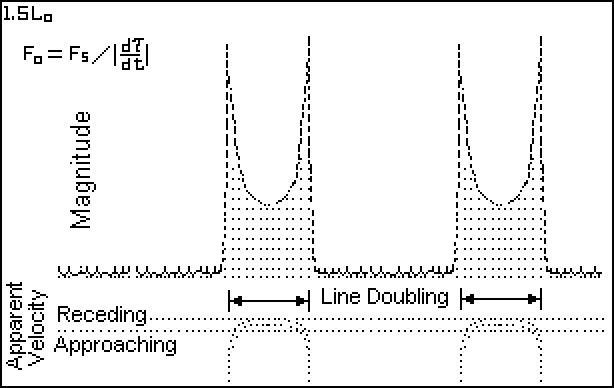
Figure 8. Lo = 1.5 L - Time Modulation

The light curve of Figure 8 bears a resemblance to that for the Geminga Soft Gamma Repeater.

Figure 9 corresponds to a binary star with both components visible. The component which produces the lower amplitude pulse has a semi-orbital diameter of 1.2 times that of the other component. This light curve is remarkably similar to that for the Crab Pulsar, as shown in Figure 10.

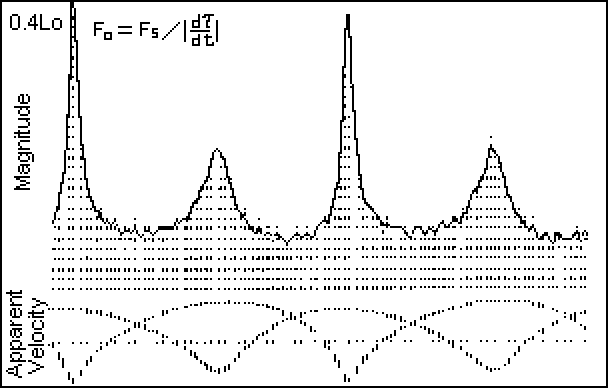
Figure 9. Lo = 0.4 L - Time Modulation

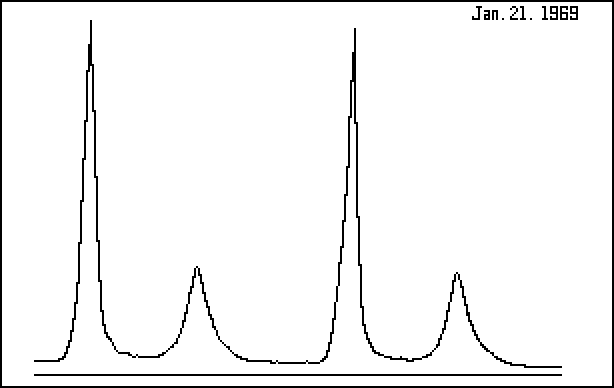
Figure 10. Crab Pulsar - NP 0532
After R. Lynds, Jan 21, 1969

The Crab Pulsar pulses may, in fact, be due to synchrotron radiation produced by a spinning neutron star. If so, both peaks should show evidence of the common stellar source. If the individual pulse spectra suggest two different sources then high speed - high resolution spectroscopy will be needed to provide us additional clues about the nature of this object. The article by Massaro, et. al., titled A two component model of the Crab pulsar emission based on the BeppoSAX pulse profiles(10) is a good step in this direction. They conclude "We have shown that the pulse shape change of [the] Crab Pulsar in the X and low-energy Gamma rays can be explained by means of a two component model. These two components must have substantially different energy spectra and phase distributions." The authors suggest that a second emission region in the neutron star's magnetosphere adds to the total energy of the X-ray and low-energy Gamma ray spectrum of the interpulse bridge and the secondary pulse.

_______

The author proposes that the Crab pulsar is comprised of a pair of neutron stars, traveling in orbits of average radius approximately 200 kilometers, (17 "Houstons") with orbital speeds on the order of 0.014c. The shape of the light curve(s) for the Crab pulsar suggests an extinction distance equal to one half the de Sitter overtaking distance L, as calculated using equation 4.

Here T would be equal to one half of the 35 msec orbital period or 17.5 msec. We get L=1.87*10e+5 km. Half of this is 9.3*10e+4 km which is about one fourth of the average earth-moon distance.

Extinction Distance versus Observer Distance

Up to now, we have been considering the distance from binary to observer in terms of a given multiple of L. This can be a bit mis-leading. It may be more proper to re-define this distance as from the binary to extinction, as discussed by Fox. Beyond this distance the light traveling to the observer will be traveling at the speed of light with respect to the dispersive interstellar medium. If the restricted Ritzian c + v hypothesis becomes validated then variable stars will provide us a tool to measure interstellar extinction distances and hence give us information about the density of interstellar matter near the sources.

It is postulated that Gamma-Ray Bursts are produced by Ritzian relativity (c+v) effects associated with close perihelion encounters of normal stars, dwarf, and/or neutron stars. For GRBs, the element of variability is, as with Cepheids and pulsars, information arrival time. It is speculated that the stars and other bodies involved in the production of GRBs are located in the disk structure of the Milky Way.

Figure 11 shows a close encounter of two stars which could lead to gamma ray flashes/bursts. Light curves for the blue component are shown for increasing distances from the encounter. For this example an extinction distance equal to 0.6 times the de Sitter overtaking distance is used. (For simplification we specify that extinction occurs suddenly at the stated distance.)

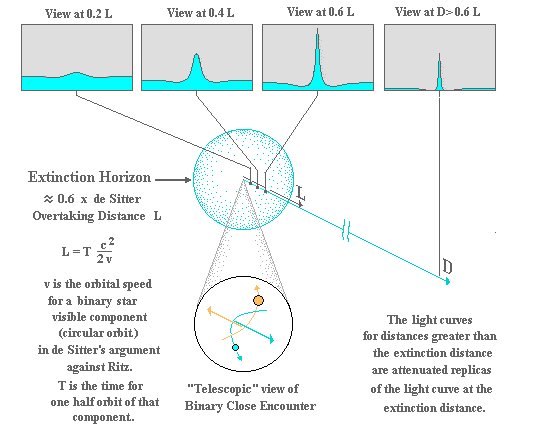
Figure 11. Simple GRB Generation

Evidence for Gamma-ray Eclipses?

Since binary star close encounters are hypothesized here, we should expect to occasionally see evidence of eclipses which block out portions of burst/flash light curves.

Figure 12, which is a marked up BATSE graph(11) for GRB 910430, demonstrates hypothetical effects of a three body interaction. Here M1, the primary, has a radius on the order of 2 -10 times that of M2. The perihelion passage of M2 provides the main part of the burst. M3, a much smaller and less massive body than M2 is orbiting M1 in such a manner that its far side swings are not totally obscured (to the distant observer) during the eclipse of M2 by the larger M1. (The gravitational effect of M2 on M3 would be to repeatedly modify its orbit with respect to M1.)

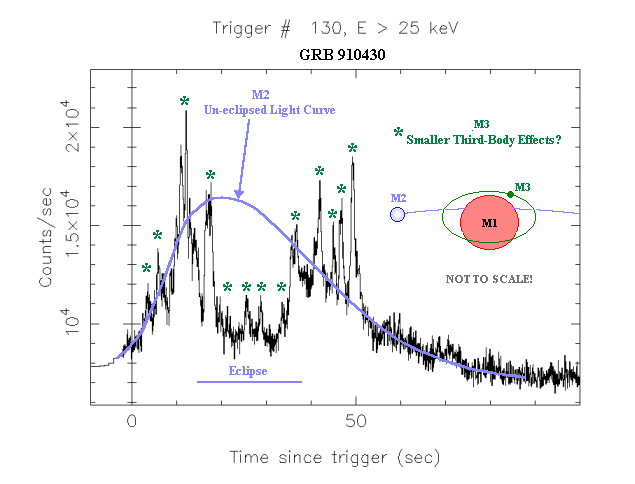
Figure 12. Three Body GRB With Eclipse

The abrupt cessation of the fine-structure spikes at t=50 sec (the suggested M3 effect) can be interpreted as M3 having being flung out of orbit from around M1, or crashing into either M1 or M2.

* * *

The author will be on hand to demonstrate computer simulations of the binary and multiple star interactions and their resultant pulsating and eruptive light curves during afternoon coffee breaks. 3.5 inch floppy disks with Quick BASIC source codes and DOS executables will be available for interested parties.

This document is available online at:
[Link no longer necessary.]

Source code (and an executable file used to produce figures 4-9)
is available at http://www.shadetreephysics.com/binaries.htm

References

(1) W. Ritz, Ann. Chim. Phys., 13, 145-275 (1908). An English translation of the Introduction and First Part of this work was privately published by the author in 1980. Portions of the translation are available on-line at http://www.shadetreephysics.com/crit/1908a.htm.
(2) R.S. Shankland, Am. J. Phys., 31, 47 (1963)
(3) W. de Sitter, Proceedings of the Section of Sciences - Koninklijke Academie van Wetenschappen -- te Amsterdam, 15, 1297 (1913).
[This is an English translation of ref (5).]
(4) W. de Sitter, Proceedings of the Section of Sciences - Koninklijke Academie van Wetenschappen -- te Amsterdam, 16, 395 (1913).
[This is an English translation of ref (6)]
(5) W. de Sitter, Physik. Zeitschr., 14, 429 (1913) http://www.shadetreephysics.com/desit-1g.htm
[An approximate English translation may be found at
http://www.shadetreephysics.com/desit-1e.htm.]
(6) W. de Sitter, Physik. Zeitschr., 14, 1267 (1913) http://www.shadetreephysics.com/desit-2g.htm
[An approximate English translation may be found at
http://www.shadetreephysics.com/desit-2e.htm.]
(7) J. Fox, Am. J. Phys., 33, 1 (1965)
(8) R. Tolman, Phys. Rev., 31, 26 (1910), ibid. 35, 136 (1912)
(9) V.I. Sekerin, Contemporary Science and Regularity in its Development, 4, 119-123, Tomsk University (1987). (In Russian.) A copy of this paper was furnished to the author via private correspondence. (An English translation is available on-line at http//www.shadetreephysics.com/sekerin.htm).
(10) E. Massaro, M. Litterio, G. Cusumano, and T. Mineo, Nucl. Phys. B - Proc. Supp., (1998) 69, 269-272.
(11) Compton Observatory BATSE Second Burst Catalog, Compact Disc, Disk 1, USA_NASA_COSSC_BATSE_0002.

"In Zeitschrift für Physik, XXI, 6, p. 333 (1924) Prof. M. La Rosa has pointed out a remarkable consequence of the theory of Ritz regarding the propagation of light, which seems not to have been noticed before. If this theory, according to which the velocity of the source is added to the velocity of light, is true, then the light emitted by a star, whose motion relatively to the observer is periodic, during equal intervals of time, will reach the observer during unequal intervals, the inequality increasing with the distance of the star. Consequently the star will appear to the observer to be variable, even if the emitted light has a constant intensity. This, of course is entirely correct, but, contrary to the opinion of Mr. La Rosa, it does not afford an argument in favour of Ritz's theory, but rather against it." [De Sitter furnishes the rationale and calculations to support his contention.]

See: de Sitter, W. Bull. Astron. Institute Netherlands, 2, 121 (1924) - NADS.

"In B.A.N. 57 I supposed that the effect of relative motion on intensity had never been noticed before Prof. La Rosa pointed it out in the beginning of this year. I have since found that it was already mentioned by Einstein in 1905 [Annalen der Physik, 17, Zur Electrodynamik bewegter Körper, § 7.]

See: de Sitter, W. Bull. Astron. Institute Netherlands, 2, 163 (1924) - NADS