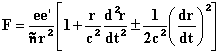Figure 1. Brightness and Apparent Radial Velocity vs Time for Lo = 0.07 L. This figure, according to Sekerin, could be for a Cepheid variable.(*) However, for Cepheids, the peak (approaching) apparent radial velocity curve coincides with the peak of the brightness curve. Sekerin's radial velocity curve lags his brightness curve by 90 degrees. (This can be fixed.)

Time

(*) Up until 1914 Cepheids were considered to be spectroscopic binaries, but following papers by Plummer and Shapley in that year, astronomers came to think of them as pulsators. See: H.C. Plummer, "Note on the Velocity of Light and Doppler's Principle," MNRAS, 74, 660 (1914) [NADS], and Harlow Shapley, "On the Nature and Cause of Cepheid Variation," Ap. J., 40, 448 (1914) [NADS]. The author of this webpage is of the opinion that Cepheids may yet turn out to be binaries (wobbly common envelope binaries) with Ritzian relativity producing the periodic brightness and spectral variations. [Added 14 Dec 2009. Updated 16 Dec 2009.]

Figure 2. Brightness and Apparent Radial Velocity vs Time for Lo = 0.72 L (de-Sitter's argument is for Lo = 1.0 L.) With later light periodically overtaking earlier light, we get . . . arrival-time modulation. These observed spikes, which could be interpreted as periodic eruptions, and would measurably be very energetic. (Sekerin would urge us to be cautious about we think we know about the source's intrinsic nature based on our observations.

Time

Figure 3. Brightness and Apparent Radial Velocity vs Time for Lo = 2.8 L The arrival time reversals produce saddle shaped brightness curves that are similar to certain light-house model pulsars. Each CRT dot represents the . . . contribution of one segment of the orbit for the visible component.

Time

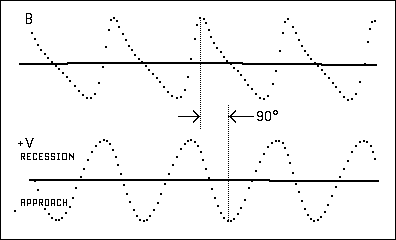
I wrote a digital computer program called D-CEPHEI which simulates Sekerin's scenario and got similar results, i.e., the 90 degree phase error between the curves. The simulation uses an ellipse generator and at selected points in the orbit the distance from a visible component to a fixed observer is "measured." Then the computed source-to-observer travel time, using either a constant speed of light or c + v is used to fill arrival time bins (buckets). The accumulating sums in these bins are scaled time-wise on the computer CRT screen. Doppler effects for each "emission point" are used to create accompanying . . . radial velocity curves. When two and a half orbits have been completed the program stops the run and adds an "envelope" showing the final summations of the arrival time bins. This envelope corresponds to what we would observe in real-time. Now, regarding the 90 degrees phase error, what sin of omission (or commission) was being committed ... besides the basic heresy of using c + v? Both computer models used Doppler shift computations to generate the radial velocity variations curve. Currently, Cepheids are said to be expanding and contracting, and the variations of their radii account for the apparent radial velocity variations. When they are expanding, we get approaching Doppler effects, and when they are contracting, we get recessional Doppler effects. Sekerin's hypothesis, in contrast, says that the apparent radial velocity variations are due to orbital Doppler effects of a binary component (in a non-extinction environment), but his curves suffer the 90 degree phase error. This phasing error, if not resolved, would invalidate his thesis. Time passed. . . . In 1991 I was explaining Sekerin's Doppler phasing dilemma to James Mallet, a British entomologist. His totally unexpected response (with regard to a genuine c + v environment) was, "But there'd be no Doppler." I made several mis-starts at trying to refute Mallet's contention but eventually was forced into silence. He was right! (At least, in part.) For a non-accelerating light source which is moving toward or away from a given observer in a c + v arena, the observer would not detect a Doppler related wavelength change, but the observed frequency would be changed by a factor of (1 + v/c) when approaching, or by (1 - v/c) when receding, but the wavelength would remain constant. [Repaired 14, 16 Dec 2009.] Top Ritz expressed this idea (about the unchanged wavelengths)* by saying that a material point (or a star in our case) moving at a constant speed emits concentric spherical wave fronts, each of which is centered on the source at its latest position. There is no bunching up of wavefronts in the forward hemisphere and no spreading out of those behind. * See Ref (1), pp 209-210 and the related Light Motion Animations. [Second link added 14 Dec 2009.] (Earlier versions of this article described an algorithm that used my erroneous idea about orbital accelerations with respect to the observer as a means to produce a properly phased apparent-radial-velocity curve. What follows is a first stab to clean up the reasoning.) For a binary star in a genuine c+v environment, observed frequency variations can be caused by the same information arrival-time-modulation that is hypothesized to cause the observed brightness variations. For observed frequencies, we have fo = fs / (dτ/dt), where fo represents the observed frequency, fs is the raw (unshifted) source frequency, and dτ/dt represents the differential of information arrival-times versus real-time. Here, τ refers to Ritzian relativity modulated light arrival-times (which will be temporally aberrant) and t refers to real time. [Last sentence added 16 Dec 2009.] For a non-accelerating source with respect to a given observer, dτ/dt = 1. [Added 31 Jan 2006] I replaced D-CEPHEI's algorithm which computes apparent-radial-velocity based on orbital accelerations with respect to the observer with one which uses the arrival-time-modulation factor dτ/dt. Since this temporal Ritzian aberration of observed frequency fo is not a Doppler effect, it should be given a name which cannot be confused with ideas associated with existing terminology. For now the phrase time modulation will be used. [This paragraph was added on 28 October 2002.] For "local" binary-to-observer distances (less than 1.0 x 10exp-5 times the de Sitter overtaking distance L) the time modulation variations turn out to be equivalent to orbital Doppler effects. If the de Sitter overtaking distance happens to be 85 light years, then the 1.0 x 10exp-5 L fraction corresponds to approximately five astronomical units. At greater distances the time modulation effect begins to produce time-wise compressions of information when the component of concern is passing through its furthest point from the observer, and a stretching-out of information when the component is passing through the closest distance to the observer. These compressions and rarefactions produce frequency shifts that are more-or-less in-step with orbital accelerations with respect to the observer. Time-wise they precede typical Doppler effects by 90 degrees. [This paragraph was re-worked on 28 October 2002.] At about 3.0 x 10exp-5 times the overtaking distance (16 AU for L= 85 LY) the 90 degrees leading time modulation effect equals that of the Doppler-like effect. (A combination of the shifts leads to an overall 45 degrees leading phase shift compared to Doppler alone.) Beyond 1.0 x 10exp-4 times the overtaking distance (54 AU for L= 85 LY) the time modulation acceleration-like effect dominates. 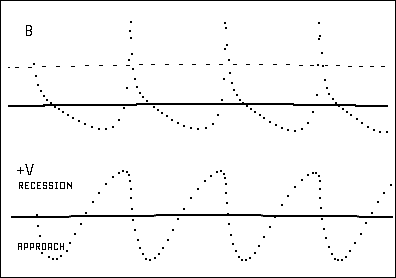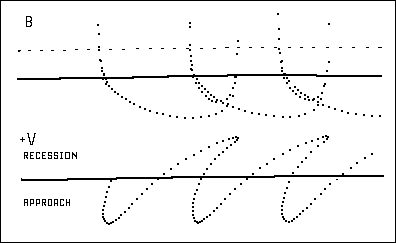As the binary-to-observer distance reaches and exceeds the de Sitter overtaking distance, the intensity and time modulation curves come to display time-reversals with line doubling bounded by infinite-frequency excursions. (See figures 8 and 10 below.) This linear relation between source-to-observer distance and the acceleration-like effects of the dτ/dt factor is reminiscent of Weber's 1846 electrodynamic expression for the forces that single electrical charges exert on each another as functions of their distances, accelerations and velocities with respect to one another. The following equation approximates Weber's expression. 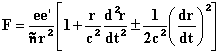(I have used a plus/minus sign (instead of his minus sign) preceding the velocity squared term.) In the mks system the constant ñ would be . I confess that the velocity squared quantity above causes me grief and that more digging into this old expression is in order. At about .00003 times the overtaking distance (16 AU for L= 85 LY) the time modulation 90 degrees leading effect equals that of the Doppler-like effect. Beyond .0001 times the overtaking distance (54 AU for L= 85 LY) the acceleration-like effect predominates. As the binary-to-observer distance reaches and exceeds the de Sitter overtaking distance, the intensity and time modulation curves come to display time-reversals with line doubling bracketed by infinite-frequency excursions. (See figures 8 and 10 below.) I digress at this point to call attention to Einstein's view on this business. The following passage is borrowed from the last paragraph of Section 2.10 of Keven Brown's Reflections on Relativity. Robert Shankland recalled Einstein telling him (in 1950) that he had himself considered an emission theory of light, similar to Ritz's theory, during the years before 1905, but he abandoned it       because he could think of no form of differential equation which could have solutions representing waves       whose velocity depended on the motion of the source. In this case the emission theory would lead to phase       relations such that the propagated light would be all badly "mixed up" and might even "back up on itself". . . For an example of this badly "mixed up" light in action, see the Elliptical-Path Ritzian Binary Animations simulation. 1 - 2 - 3 - 4 - Next