This article has the following sections.
A Ritzian Interpretation of Variable Stars
Non-pulsating Cepheid Variables
Ritzian Gamma-Ray Bursts
Ultra High Energy Cosmic Rays
Modeling Geminga
Unsung Binaries and de Sitter's Whimsical Images?
GRB 790731 and omega Geminorum
Non-pulsating Cepheid Variables
(Original Title: Cepheids. It gets worse!)
Installed 6 June 1999 - Latest update 20 Jan 2010
Copies of this supplement were distributed at the Galileo Back In Italy II conference in Bologna Italy 26-28 May 1999.
Robert S. Fritzius
Vladimir Sekerin felt he could explain Cepheid variables using Ritz's c+v effects. This page is a continuation of that idea.
Special Note
The cyclic color changes of Cepheid variables appear to be consistent with Ritz c+v information arrival time modulation. This modulation is such that during a brightness peak there is a time-wise compression of the observed spectrum, which produces higher observed frequencies. If there were to be evenly spaced time markers impressed on the luminous flux (at the source) we would see that their time-wise spacing decreases during the bright phase, reaching minimum separation at the brightness peak. During the lower intensity "trough" of the light curve the time markers would be stretching further apart, reaching maximum separation at minimum intensity. As the arrival time "clock" varies in speed, the stellar spectrum changes in color (Hottest at peak, coolest at trough.) Here, we are considering a bright star with a dim (mostly unseen) companion.
Figure 1 shows five Ritzian light curves. The first is for a visible component with orbit eccentricity e = 0. The last four are for the same component but with e = 0.15 and with different perihelion positions. (The orbit shapes are exaggerated to show their orientations with respect to the line of sight to the observer.) For each of these, the visible component is shown in the orbit position corresponding to maximum brightness and maximum apparent radial velocity as seen by the observer. (According to the Ritzian hypothesis these maxima occur when the component's acceleration with respect to the observer is greatest.)
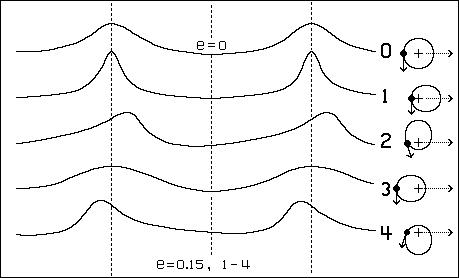
Figure 1. Ritzian (Linear Scale) Light Curves
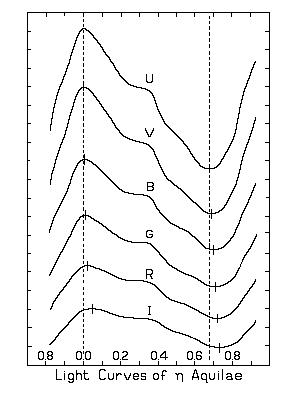
About 90 percent of published Cepheid variable light curves resemble case (4), fast rise-slow decay (FRSD). About 10 percent present symmetrical curves that that could be classified as either case 1 or case 3. In the Cepheid variable studies I have seen, Case 2 slow rise-fast decay (SRFD), light curves are extremely rare, less than one percent and those published are very close to being symmetrical.
The extinction theorem predicts that higher frequencies (this has to be qualified) will have longer extinction lengths than lower frequencies. This is based on the idea that electrical charges in the interstellar medium interact less readily with higher frequency electromagnetic perturbations than with lower frequency perturbations.
[The next paragraph still contains a good measure of wrong think. It would be sort of OK for a binary system that is approaching us. RSF 26 Oct 2003]
Starting from this premise it can be inferred that higher frequency parts of the "squeezed" light will travel further before reaching extinction. . . . The overall effect of this frequency-dependent speed of light differential will be to cause the higher-frequency components to arrive earlier than the lower-frequency components. This arrival time "skewing" is proposed as the mechanism which may be moving cases 1, 2, and 3 in the direction of case 4 (FRSD). Cepheid variables with greater FRSD effects may tend to be located in regions of space with greater extinction lengths. [This paragraph is a combination of two former paragraphs with some "B.S." (bad science) removed. RSF 28 June 2002]
The following fiture shows light curves of the Cepheid Variable Eta Aquilae, HD 187929.
(Spectral type F6-G2.) From Stebbins, Kron, and Smith(1).
U = Ultraviolet, V = Violet, B = Blue, G = Green, R = Red, I = Infra-Red.