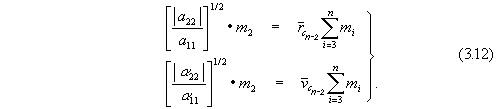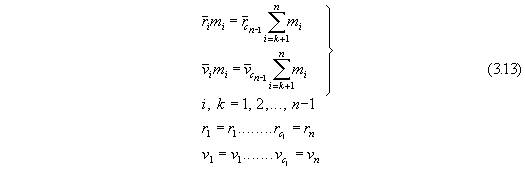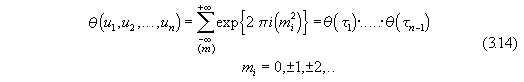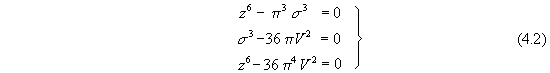|
Page 163
From (3.8) we obtain the second equation of the center of gravity for the
first sub-system...
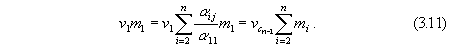
It follows, from the equations for the general center of gravity, that the
values of the sums
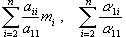 are independent of the (moment) t0 at which we are
observing the system.
are independent of the (moment) t0 at which we are
observing the system.
Equations of the center of gravity of Newton's second sub-system can be
obtained from the second components of the quadratic forms (3.7) and (3.8)
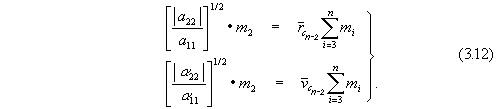
This (consists of) a body of mass m2 and a general center
of gravity for n-2 bodies. The line of action of forces of the
second sub-system is othogonal to the line of the first, and the resultant
of forces of the interaction of a body of mass m1 with
bodies m2 and
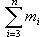 is applied exactly (to) the general center of gravity of the latter.
is applied exactly (to) the general center of gravity of the latter.
If the system is for three bodies, then the reduction is complete.
Transformation of (forms) (3.7, 3.8) to the main axes releases pairs of
bodies from acting on one another (Theorem XXIV). From the equations for
the centers of gravity of Newton's sub-systems
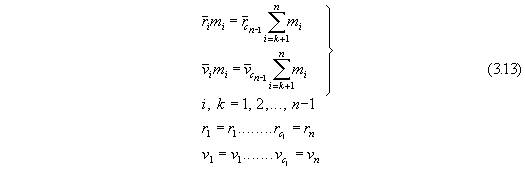
Page 164
are calculated semi-axes of Kepler's orbit aibi, on
which μi bodies are moving. Orbits of bodies with masses
m1, m2 are built as free
(multiplications) of n-1 Keplerian orbits.
In this way, the problem of n bodies with any
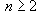 is integrated in an elliptical coordinate system.
is integrated in an elliptical coordinate system.
For the definition of the orbit for any body of that system, it is
necessary and sufficient to look at n/2 (n is even) or
(n+1)/2 (n is odd) expressions of quadratic form, by changing
(numerization) of the bodies by cyclic (permutations) (by twos).
The equations of the orbits are represented by Abel's
θ-functions for n-1 variables, which are, because of
the diagonality of the quadratic forms, free (multiplications) of
n-1 Jacobi's ellipical functions.
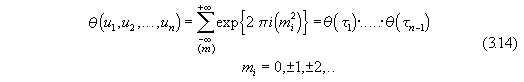
The problem of three bodies in a straight line was examined first by Euler
[19] and then by Lagrange [38], and is characterized by coefficients
 ,
that give the (transformation) of a system of three bodies into two free
sub-systems, (which) are represented as non-real (one line of forces
(acting)). Lagrange's system of three bodies with ,
that give the (transformation) of a system of three bodies into two free
sub-systems, (which) are represented as non-real (one line of forces
(acting)). Lagrange's system of three bodies with
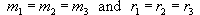 [39] during (diagonalization) of the quadratic forms are divided (into)
free bodies which don't act on one another, the same, as with similar
systems of four and six bodies.
[39] during (diagonalization) of the quadratic forms are divided (into)
free bodies which don't act on one another, the same, as with similar
systems of four and six bodies.
4. Comparison of obtained results with (classical)
Let us compare between obtained results and (classical). The solution of
the n-body problem should satisfy the theorem of Bruns-Poincaré,
i.e., (it) should be defined by 10 general integrals of motion - six
coordinates for the centers of gravity, three Keplers and an integral of
energy or (activity) S. Of these 10 integrals, six are linearly
independent. All other integrals - for example, the 18 particular integrals
of the three-body problem - with
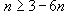 , should
be linear (transformations) of these six. , should
be linear (transformations) of these six.
Let us do once again the separation of n-1 minima of quadratic form
(3.8) on the axis of Descartes coordinates, according to Jacobi. Each of the
component-minima, in expression (2.3), is related to the periods of the
θ-functions.
Page 165
Their free multiplication defines a structure of general and of particular
solutions of the problem. In this way a number of constants, shown by the
Bruns-Poincaré theorem, is exactly the same with any
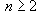 as (the) number of constants, which define the obtained solutions. So, with any
as (the) number of constants, which define the obtained solutions. So, with any
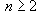 all 6n coordinates of the centers of gravity, 3n of Kepler's
and n in particular integrals of energy, become linear transformations
(of) one from ten general, and the n-body problem is (for) any
all 6n coordinates of the centers of gravity, 3n of Kepler's
and n in particular integrals of energy, become linear transformations
(of) one from ten general, and the n-body problem is (for) any
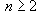 ,
a problem of 6th order (look at [19]). These particular integrals are
obtained as a result of bringing the quadratic (forms) (activity) toward the
main axes and represent, by themselves, solutions of canonical equations,
which totally correspond to the Hamilton-Jacobi theorem [31]. ,
a problem of 6th order (look at [19]). These particular integrals are
obtained as a result of bringing the quadratic (forms) (activity) toward the
main axes and represent, by themselves, solutions of canonical equations,
which totally correspond to the Hamilton-Jacobi theorem [31].
Theorem
If the Hamilton-Jocobi solution S(Qq) is already known, and that
solution is dependent on n parameters and is such that
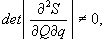 then the canonical equations
then the canonical equations
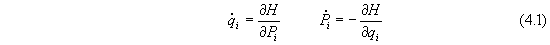
are solvable explicitly in quadrature.
Let us look at isoparametric equations (see [42])
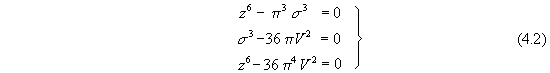
where
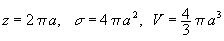
which define the harmony of physical and geometrical spaces on one, two
or three dimensions. (The) dimension(s) of (the) absolutely invariant in
R3 - (a) determinant in quadratic form, corresponds to the
space(s) of (Liouville) [31], which (have) the dimensions of a cube of
(activity). According to this, we, naturally, can suppose that
a2 is proportional to the (activity) of the system.
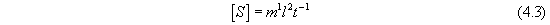
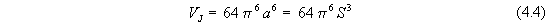
Let us notice that an increase in the dimensions of space, for example,
a change in phase [31], will cause the creation of integrals of motion
that do not appear in any of the three classes that are given by the
Bruns-Poincaré theorem, as well as changing of the physical dimensions of
the integrals of motion,and this will cause the (condition) in which it will
be impossible to integrate the problem.
|
|