By using the qualities of conic sections and proportions, Newton brings the system of two bodies with masses m1 and m2, that are acting on each other to the system of one body in free motion. In the beginning, instead of attraction between them, comes attraction to their general center of gravity (Theorem XXIV), then the non-moving point transfers to "the center of gravity of the largest and most internal body" m1 (reduction and Theorem XXIV), and orbits of (points) with masses m1 + m2 and m2(?) are built (Theorems XX, XXII, XXIII). Then, the imovable point is transferred to the general "center of gravity of the two internal bodies," and we obtain the orbit of a point with a mass μ. The orbit of the μ-point, an ellipse, (with time) becomes a circle with (the) radius of the larger semi-axis, so the motion of the μ-point will be without acceleration. For this reason, Newton introduced projective coordinates, i.e., {they transform a metric to a straight interconnected body}.
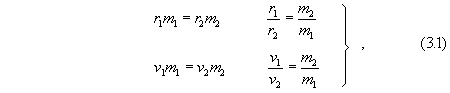
Page 160
From (3.1), by using proportions
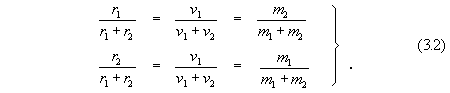
By using r1+r1 = r12 , v1+v1 = v12 we obtain
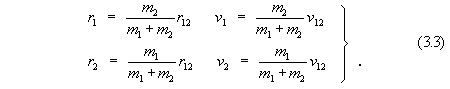
Substituting (3.3) into (3.1) gives
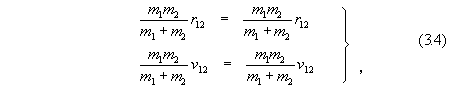
which formally defines the system of two bodies of equal mass
Quantities (3.3) are (projective) coordinates on the interval (simplex)
[38] invariant relative to the translation of the (system). The
values of μ, r12 and v12 allow
us to find the semi-axes of the conic section - ellipses a and
b, the values for which define the coefficient of a quadratic form
in the elliptic θ-function of Jacobi [41].
b. The Problem of n Bodies
Let us look on the problem of n bodies. For its solution it is
necessary and sufficient to transform, by using Newton's laws, a series of
n bodies acting on each other, into a system of a finite (number) of
Newton's sub-systems, each one with two bodies. This is done by
using the {main axes of quadratic form} -- a metric that is induced in
R3 by a system of n bodies, that at the moment of
time t0 are polyhedra, located at the n centers of
gravity of the bodies.
We will (put in) (three) second power linear forms, defined as the sum of
the projections of radius-vectors of bodies onto the axes of a Descartes
system of coordinates, with the origin in the general center of
gravity of all systems.
Page 161
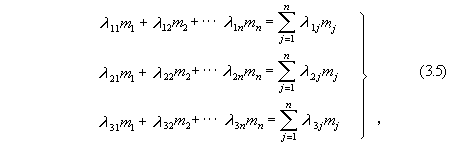
that gives the expression
where
are second powers of radius vectors ri.
-- their scalar products, which are proportional to the projections of the
ith vector on the jth, mi - masses that
normalize the values of the vectors ri.
Let us notice that ri(aii)1/2 are
the lines of force (activity) which attract the bodies to the general center
of gravity of the system, and values of aij define how
much that a given system is distinguished from a free system, i.e.,
proportional to the actions of the bodies on one another.
Let us bring the quadratic form to the main axes ([27] p. 389).
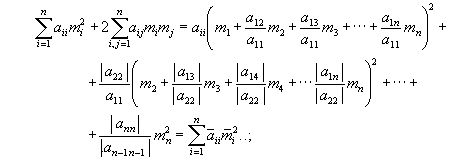
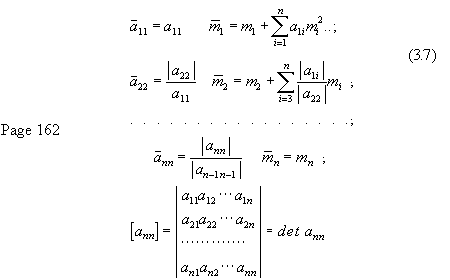
Expression (3.7), from a formal point of view, appears to represent the
sum of orthogonal vectors, because of the mute absense of component species
aij mi mj . But in
R3 it is only possible to orthogonalize a system of three
vectors. Thus, we should look on the transformation of that form to the
main axes as a transformation of a polyhedron, as a result of which the
algebraic sums of aij mi mj will be
zero. It is canonical [31], and transfers the n-body system with
masses m1, m2, . . . mn,
that act on one another, to a system of n bodies with masses
m1, m2,...mn, on
which only the general center of gravity of the system acts ([1], Theorem
XXIV).
In a similar way, it is possible to transform the quadratic (form), built on
weighted velocities
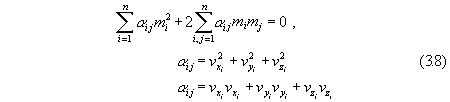
The zero components of the quadratic forms, (are) transferred to the main
axes of the centers of gravity of (n-1) Newtonian subsystems of
n bodies.
Let us look on the first component in (3.7). It (transfers) (to) zero
because of the inequality
From this we obtain the first equation of the center of gravity of the first
Newtonian sub-system of two bodies - a body with mass m
from the general center of gravity for system Cn .
