1. Introduction
Considering the problem of the integration of differential equations, the solutions of which represent trajectories in a system of n bodies, let us adopt a revision of the problem which is maximally close to Newton's [methods] [1].
Let n bodies, considered as material points with masses m1, m2, . . . mn, to be moving under the influences of attractive interactive forces, directly proportional to the absolute forces and inversely proportional to the squared distances between them. By assigning for the moment of time t0 their coordinates and velocities we will try to find their equations of motion.
In paper [2] we considered the general positions of classical mechanics from the point of view of the the theory of manifold transforms, which represent, in appearance, a geometrical method of solutions of the differential equations of dynamics. This made it possible to formulate a theorem which can prove the solvability of the n body problem in elliptical quadratures. As a concrete expedient, the reduced mass method was pointed out ([2] p. 320)., a discussion which is also addressed in the present work. Since the basis of this most recent method lies in the theory of conic sections and proportions, let us begin with a short review of their development. [3-9]
The compositions of simple conic sections, circumfrences, which determine perfect circular motions, were used even by the ancient Greeks for the construction of the complicated visible trajectories of the heavenly bodies -- the revolution of the spheres, each set inside the other [10]. Such are the kinematic schems of Eudoxus of Cnidus, Hipparchus-Ptolemy [11] and Copernicus [12]. Kepler's elliptical orbit is also a composition of two circular motions [14].
In Newton's Principia, the mathematical apparatus which consists of the theory of conic sections and proportions [3, 15, 16], elliptical motion is reduced to circular ([1], p. 101), i.e.,
Page 156
uniformily accelerated. By measuring all motions in that way, Newton changes
all curved spaces (metrics to Absolute Euclidian and so forth. Newton's
three laws of mechanics are rightfully just like the invariableness of a
system of n bodies relative to three linear transformations: The First
Law - invariableness relative to parabolic transformations, the Second Law -
relative to elliptical transformations and the Third Law - relative to
hyperbolic transformations; corresponding to the three classic conic sections.
This allows us to bring those conic sections from general conditions, to
particular - to the circle and straight line.
Euler departs (although not totally [17] from Newton's methods, in expounding
analytical mechanics, using differential equation, for the first time, in
order to determine the trajectories for problems with two or three bodies
[18]. By using that way, he obtained a series of fundamental solutions, in
particular, the problem of n bodies was defined as a problem of sixth
order for any n, and all integrals of motion were determined -
invariants, which determined the dynamics of a system of n bodies with
n >= 2, [19] (See the Bruns-Poincaré theorem) [20, 21, 22]).
Yet, precisely in connection with his working up of the theory of differential
equations, Euler proved the theorem of elliptical differentials [23], which
is a first step towards a general theory of conic sections, setting up a law
of their composition as simple events. Future developments of this, as in
the theory of Abel's (θ?) functions [3-9], takes that theorem as a starting point.
To Euler belongs the arrangements of the main positions in the theory of
surfaces [24], which was developed later by Monge [25] (with the use of
characteristic coordinates [26]), which from Poincaré's interpretation [9],
united with the conic sections in the theory of Abel's θ-functions.
The methods of Abel's θ-functions allows us to give analytical
expressions for a surface, which is a transfer surface (compare with
[24, 25] and [91]) - a general solution of differential equations, and
particular solutions - the integral curve through integration of motion
of the problem, is similar to the expression of classical conic sections
via the constants of Apollonius [4]. The methods of diagonalizing quadratic
forms, developed by A. N. Korkin and E. I. Zolotarev [27], allow us to
represent the algebraic curve of the integral of a manifold in the form of
a free product of a finite number of classical conic sections (Lie's group
represents a free product of mono-parametric sub-groups [28, 29], i.e., we
can reduce the n body problem to the solution of a finite number of
Newton's two body systems. Such a thing is possible for any n.
Page 157
2. Linear Transformations,
Geometrical and Force Relationships
Theorem
If a group, induced on the basis of coordinate functions, is isomorphic to the group of motions (a Lie group) of a dynamic system, which is described by a given differential equation, then the latter can be solved with quadratures (usually elliptically [8, 9]) independently of the group structure.
And, in reality, the {projectivization} of a manifold transforms the differential equations of geodesics, the non-linear equations of Newton, to total differentials ([32, 33], {ct.} [34]), (because) the components of integrations are inside the structure of the coordinates, which are given by a complicated proportion [35, 36].
The equation of the projective model of algebraic curves, i.e., the general solution of the differential equations of motion, is given by Abel's θ-function [6, 9].
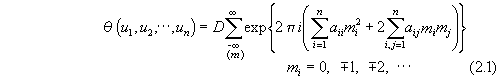
Where
![]() is the square of the radius of an absolute sphere, inside which is
is the square of the radius of an absolute sphere, inside which is
located the real part of Lobachevsky's three dimensional space [37], and
D is a constant.
With concrete values of D and aij (2.1) defines an
integral curve, located on the surface of a cone (a section of a conic
integral surface).
![]()
Diagonalization of the quadratic form (2.2) leads from expression (2.1) to a free multiplication of Jacobi's elliptical θ-functions, which then represents an invariant form of writing a conic section (compare to [4] ).
![]()
Page 158
Elliptical θ-functions are the basic characteristic coordinates
of the n-body problem (the n-body system has, as characteristic
coordinates, free multiplications of n-1 elliptical
θ-functions or Abel's θ-functions from
n-1 variables).
We can look at expression (2.3) as an invariant form of the Phythagorem
theorem or Euler's theory about the axes of motion of a solid rigid body
[28].
During diagonalization, a determinant of quadratic form, which has the
dimensions of squared volume, keeps its (magnitude). Since all imaginary
quantities in the projective model of Lobachevsky spaces [37] are defined
through the related real values [35], then the functions which define
transformations and solutions are analytic.
The invariance of (2.2) relative to linear transformations allows us to
deform an arbitrary polyhedron, assigned for any moment of time
t0 to vertices at the centers of gravity of the bodies
such that the geometric centers [38], i.e., centers of ribs, of facets,
which contain its simplexes and sub-polyhedra will coincide with the
centers of gravity of pairs of bodies, of triplets of bodies and so on, and
in the centers of application of the forces. Then, the relations of masses
and distances, as well as the relations between masses and velocities, will
satisfy Newton's theorems. Those points will be defined by zeroes of the
θ-functions, as well as the centers of the bodies, i.e., they
will belong to the integral surface, a transfer surface, that is given by
Poincaré's equation [9].
![]()
Compare this with Newton's remark about the proportionality of distances in
the problem of 3 and n bodies [1], theorem XXV, XXVII, pp 222-243
and with the memoirs of Lagrange [39, 40] ).
3. The reduced mass method in the problem of n bodies
a. The problem of two bodies
Let us consider in detail a solution of the problem of two bodies by the reduced mass method as a result of performing the first two steps of Newton's reduction, which defines the algorithm for the solution with arbitrary n ([1], p. 242), (using) theorems that are corollaries of the three laws and the attributes of conic sections.
Theorem XX
Two mutually attracting bodies describe similar trajectories both about their common center of gravity and about each other.
Theorem XXI
If two bodies are mutually attracted by whatever kind of force and thus are revolving around their center of gravity,
Page 159
then I claim that under the influence of the same force, each body is
permitted to describe a figure around an immovable body, equal and similar
to those that they describe one about the other.
Corollary 2
Two bodies that are attracted to each other with a force that is
indirectly proportional to the square of the distance between them, will
describe conic sections around their center of gravity and about each other.
Theorem XXIV
If two bodies that are attracted to one another with any force, without
influence of other forces, are moving, their motion will be the same as in
the the case in which there is no force between these two bodies, but they
are attracted by a third body, located at their center of gravity, with
the same power.
The transformations, defined by the theorems, are important for the creation
of a reduction which will give a solution of the n-body problem, done
by Newton ( [1] Conclusion -- Theorems XXVII {suggested by} XVII, p. 242),
as a rule for orbit foci locations:
"The focus of each orbit should be taken at the general center of gravity
of all internal bodies (i.e., the focus of the first and most internal orbit
should be taken as the center of gravity of the largest and most internal
body, the focus of the second orbit - at the center of gravity of the two
internal bodies, the focus of the third orbit - in the center of gravity of
the three internal bodies and so on)".