The remarkable experiments of Kaufmann on the electric and magnetic deviability of &beta rays from radium

Annales 190

have lead to the belief that the mass of corpuscles or electrons depends on their velocity and is entirely of electromagnetic origin. The existence of an electric inertial reaction and its variability with velocity was anticipated by the theory which at a first glance seems to have received a remarkable confirmation. However in view of the scope of these conclusions it is advisable to find out if they are absolutely indispensable.
      Let's recall that in these experiments a beam of β rays is simultaneously subjected to the action of an electric field E, producing a deviation y, and to a magnetic field H parallel to E, producing a deviation z perpendicular to the first. A photographic plate, perpendicular to the non-deviated rays, records an impression of the rays, and permits a direct measurement of y and (Oeuvres 355) of z. With m and v the mass and velocity of an electron, e its charge, and a and b two constants of the apparatus. We have, according to Lorentz's theory,

      Radium, within certain limits, emits rays of all velocities. These equations, where v plays a parametric role, represent a certain parabola if m doesn't depend on v. But the curve observed by Kaufmann is different. This occurrence calls for various explanations.
      1° According to Lorentz, the movement of an electrified body with respect to the ether is equivalent to an electric current whose field, by an effect analogous to self induction, reacts on the body and produces a force which, in the most general hypotheses, is a linear function of the acceleration components, the coefficients (for transverse and longitudinal mass) being functions determined by the absolute velocity v known, for example, for the sphere and ellipsoid. In the case of Kaufmann's

Annales 191

experiments, only the transverse mass comes into play. If we use the function in (16) instead of m we very closely approximate the observed curve, whether we consider the electron as a rigid sphere (Abraham) or whether we only consider its volume to be constant (Bucherer and Langevin).
      To appreciate the value of this interpretation let's recall that the calculation of electrodynamic mass relies uniquely on the motion of the electrified body with respect to the ether, the position and velocity of other bodies being of no consequence. It is the body's absolute velocity which is used in the formula Under this interpretation Kaufmann's experiment will be therefore the first to present evidence of absolute motion. Now, regarding this delicate question, Lorentz's theory, at least in the form as expressed in section 1, is in disaccord with the experiment, and this disaccord carries over in particular to the expression of electromagnetic momentum G (1), from which Abraham (Oeuvres 356) has deduced values for longitudinal and transverse masses. Indeed, from the calculation of G we deduce(2), for the case of a charged condenser carried along by the earth's translational motion, the existence of a second order couple impressed on the condenser. But Trouton and Noble, who did this experiment(3), didn't observe the couple. Therefore the quantity G doesn't depend on the absolute velocity or, at least not in the same manner as in Lorentz's theory. We have to conclude that, even if the agreement between Abraham's theory and Kaufmann's experiments were perfect, this theory should nonetheless be considered as doubtful.

---

      (1) The vector is, as we know, the integral of the radiant vector extended over all space, multiplied by .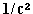
      (2) H.A. LORENTZ, Elektronentheorie,   p. 257.
      (3) London Trans., A. t. CCII, 1903,   p. 165.

Annales 192

      2° In striving to eliminate the influence of absolute motion in his equations Lorentz was led to certain new hypotheses, to which I will return in the next section. The dimensions of electrons, in particular, would be reduced to of their value when animated by the absolute velocity p. This hypothesis leads to new formulas for mass that Kaufmann considered as irreconcilable with his last experiments.(1) But this conclusion seems doubtful to me. Indeed, let's take for H, E, a, b, the directly observed values, where instead of the

(Oeuvres 357)

.

---

      (1) Annalen der Physik., t. XIX, 1906, p. 487; see also M. PLANCK, Physik. Zeitschr., t. VII, 1906, p. 754.

Annales 193

these values on the curve, fig. 11, of Kaufmann. That savant has done direct observations and then using the method of least squares deduced from the various proposed formulas a certain constant ; independent of the hypotheses developed on ; Lorentz's formula giving an inadmissible value. Our calculation shows that the value of , determined in this manner, involves a considerable uncertainty, for we took the directly observed value, and the errors that result don't exceed the admissible magnitude. As to the value its application to the &beta rays of radium can't be permitted, since it is not, in general, applicable for the Zeeman effect.
      In short, these observations don't therefore permit the preference of any one of these formulas over another, and it would be easy to expand on this more so.
      But it is important to observe that Lorentz's new hypotheses involve a modification in the expression for the force that two moving electrified bodies exert on one another, a modification which, as shown in a simple argument, is only appreciable for velocities comparable to that of light. That is to say, for Kaufmann's experiment only.
      3° This leads to a general remark. It is easy to introduce the terms presenting this peculiarity into the equations of electrodynamics. Since the system of equations (I) to (IV) can be replaced by elementary actions, it suffices to consider them here. Now the force exerted by the particle e', having velocity v', (Oeuvres 358) on the particle e, having velocity v, is expressed in this latter approach in a linear form with the factor . It is expressed in the former for the case of uniform motion, in a very complicated form

Annales 194

(given by Schwarzschild). We saw, in section 6, the first terms of the expansion for when v'/c is small. The dissymmetry established thusly between v and v' is not confirmed by experiment, and there are, as we will see in the Second Part, an infinity of formulas containing only relative velocities and consequently differing from that of Lorentz by the terms in . For a better reason, we can add the terms containing v/c, of the third and fourth orders, without which the formulas fail to be in accord with all the experiments when v/c is small. Lorentz's elementary actions formula can be only the beginning of a serial development. We will be able to dispose of the arbitrary function v thus introduced in (16) in order to produce agreement with Kaufmann's experiments by the hypothesis of constant mass, and in a manner so as to completely safeguard the relativity of motion. This is what will be shown in greater detail in the Second Part of this work.
      But there is more. The very form of the curve, and the existence of a point, where the deviations y and z are null, and the velocity equal to c, remain doubtful. Indeed, let's suppose

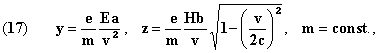
from whence [we get] the parabola

Annales 195

comparable parabola

      The values of E, H, a, b, being those given by Kaufmann, and , and for the refined values of y', z', Kaufmann (loc. cit., p. 529), the parabola becomes

                                         y' calc. - y' obs.

           z'           y' obs.          I.             II.
         0.1350         0.0246        +0.0015        +0.0014
         0.1919         0.0376        -0.0011        -0.0009
         0.2400         0.0502        -0.0022        -0.0018 
         0.2890         0.0645        -0.0020        -0.0011
         0.3359         0.0811        -0.0020        -0.0007
         0.3832         0.1001        -0.0025        -0.0008
         0.4305         0.1205        -0.0015        -0.0010
         0.4735         0.1405        +0.0002        +0.0030
         0.5252         0.1667        +0.0025        +0.0063

      The difference between the various individual values of y' observed by Kaufmann and the curve which represents the average for his experiments is often greater than 0.0030. The third column errors, although systematic, must therefore be considered as admissible. Those in the fourth column, which correspond to the hypothesis

Annales 196

to say, by 0.0034. These last points have been observed only two times and Kaufmann observes that we are inclined, at the extremities of the curve where the intensity is weak, to scrutinize the extension, that is to say the tangent, where there results a value too weak for y'. These two considerations would be sufficient to explain the errors in the fourth column. But, in this curve for (17), the critical aspect is not the velocity of light c, but the maximum relative velocity (Oeuvres 360) 2c of two light rays within the same fixed system, for which there is nothing surprising in a theory which considers only relative velocities.
      The magnetic deviation z' is nil at this point, but not the electric deviation, which is almost equal to half the width (0.03) of the curve.
      We see how expansive the field is which remains for hypotheses.
      In closing, let's note that the velocity v simply performs a parametric role, and is determined from each point on the curve by means of observed values of y and z. The result differs according to the theory used, and we can represent a curve in an infinite number of ways for a given parameter. It would be otherwise if direct and precise experiments, such as the ones executed by Des Coudres and Wiechert through the means of Hertzian oscillations on cathode rays, could give a direct determination of v, but such experiments don't seem realizable.
      Kaufmann's experiments can equally be interpreted by modifying the existing laws of electrodynamics in a manner that eliminates absolute motion and by making the electrodynamic mass constant. We can no longer conclude from these experiments that the mass of electrons is of electromagnetic origin; but it remains possible and the unity of

Annales 197

physical forces gains by this hypothesis. No matter which theory is used, these experiments will play a very important role.