Home | Up
one level | Previous | Next
Table of Contents | Previous Section | Next Section
Table of Contents | Previous Section | Next Section
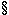7. – ANALOGY BETWEEN ETHER AND ELASTIC BODIES
WALTER RITZ
Translated (1980) from Recherches critiques sur l'Ėlectrodynamique
Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.
Annales 186 (Oeuvres 351)
Maxwell’s and Lorentz’s equations take, in the case of pure ether, a form remarkably analogous to the ones for the equations of elasticity. What is the real significance of this analogy?
The electric vector E is satisfied in ether by the equations
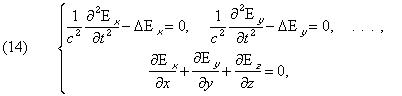
and likewise for H. This is the immediate consequence of the fundamental equations (I) through (IV).
On the other hand, the components of displacement, ξ, η, ζ, assumed to be small with respect to a point in the elastic body, A and B being constants, and m the density; we have
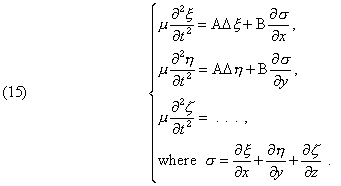
(Oeuvres 352)
Electromagnetic theory shows, as we know, that E is identical to Fresnel’s vector, H to Neuman’s vector (parallel to the plane of polarization). This identity with systems (14) and (15) leads to an elastic
theory of light. To do that, we have to admit either the incompressibility of ether, that is to say the condition
or the condition A + B = 0. In both cases, the identification is immediate. These two ways of explaining the non-existence of longitudinal waves have been admitted. In each of these hypotheses we could again choose between Fresnel’s theory which leads to identifying the speed
of ether with E, or Neumann’s theory which replaces E with H.
What are the general conditions, necessary and sufficient, such that a physical phenomenon, characterized by a vector, will follow the laws expressed in (15)? I say that they are the following:
1. The phenomenon is reversible.
2. x, h, z satisfy a system of three partial differential equations which are of second order at most, and at least are linear to a first approximation.
3. The medium is isotropic and homogeneous.
Indeed, in considering reversibility, the equations don’t have first derivatives with respect to time; we will be able to solve them by means of their second derivatives
which are vector components. Considering homogeneity, the right hand terms will have constant coefficients, and considering isotropy they will be the summations of vector components that were obtained by differentiation of x, h, z with respect
to x, y, z. But Burkhardt1(Oeuvres 353) has determined all of these vectors. When we admit only the first and second derivatives, only three exist which are linearly independent, namely
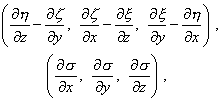
and we will have, a, b, c being constants,
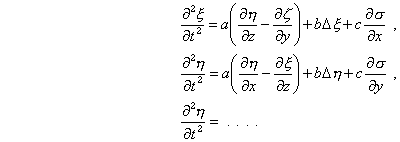
In changing the signs of x, y, z, and keeping in mind the complete isotropy, we find a = 0. Therefore only system (15) remains, Q.E.D.
Condition(1) is satisfied by all mechanical phenomena (and we have seen that in reality it shouldn’t be satisfied by electromagnetic equations which correspond to irreversible phenomena); (2) and (3) are satisfied by the phenomena of diffusion, heat propagation, and others which certainly don’t present any natural connection between them. We will conclude that the analogy between (14) and (15) is a lot less characteristic than we would be inclined to believe at first. We won’t conclude that there’s any real physical connection between the two orders of phenomena unless the analogy carries over even beyond this general analytical
form. But this is precisely not the case. Indeed, the hypothesis of the nil speed of propagation for longitudinal waves (A + B = 0) is not, as Green and Cauchy have previously said, admissible for a finite elastic body; such a body would not offer any resistance to compression, its equilibrium would be unstable. It is only recently that Lord Kelvin’s gyrostatic ether has permitted us to devise such systems. On the other hand, the hypothesis of incompressibility (Oeuvres 354) calls for the introduction to the equations one of Lagrange’s factors, performing the role of pressure. The identification is no longer possible in the cases where the pressure is constant. Finally, the limiting conditions demanded by Optics are not the same as in the theory of elasticity.
I don’t believe therefore that we should consider a priori these analogies as indicative of profound physical agreement between the two domains. If we adopt this conclusion, we won’t be overly amazed at the difficulties and strangeness that accompany all attempts made to extend these analogies of pure ether (where Maxwell’s equations express only the fact of uniform propagation) to reciprocal actions of electric charges and the ether, expressed in the general equations (I) thru (VI). For this part of the question, I can do no more that return to the chapter which Poincaré has dedicated in his Lessons2 to the most remarkable, it seems, of these attempts: that of Larmor.
1 BURKHARDT, Math. Annalen, vol. 43, 1893, p. 197; Enzyclop. D. math. Wiss., Bd. 4, Art. 14, 1901, p. 20.
2 Électricité et Optique, 2nd ed., p. 577 and following. – LARMOR, Aether and Matter, Cambridge, 1900.
Table of Contents |
Previous Section | Next Section
Home | Up one level |
Previous | Next