In placing the hypothesis of ether at the base of electrodynamics and optics we of necessity introduce, at least for the propagation of light and electric actions, a system of coordinates, independent of ordinary matter. We should therefore expect, and we have indeed long expected, an influence of absolute motion with respect to the assumed ether. We know that the experiments have always been negative. Lorentz's theory gives this result when we consider first order terms; but the experiments (Oeuvres 361) of Michelson and Morley, Trouton and Noble, and Lord Rayleigh, which should have shown second order effects, have, contrary to the theory, also given negative results. Lorentz and FitzGerald have therefore assumed that all bodies experience a contraction of the relation in the direction of their velocity v. We thus account for the observed negative results.(1) To explain this contraction, Lorentz calls to mind that, according to his theory, for a system of electric charges S, at rest, in equilibrium, this same system, when

---

      (1) M. Planck has shown that if we assume that the density of the ether at the earth's surface is less than 50,000 times greater than that in the interplanetary medium, without any appreciable change in its properties resulting, we may possibly reconcile the aberration theory with the hypothesis that the ether is entrained in the earth's motion (see LORENTZ, Enzyklop. math. Wiss., vol 5, art. 133, p. 104). This would be a very strange property of the ether.

Annales 198

assumed to be animated by a uniform translational motion v, will still be in equilibrium if we modify its dimensions by the indicated ratio. Therefore, if the molecular actions obey the law of electrostatic actions, and if we can exclude the molecular motion, the molecules of a solid body should of necessity take the position of equilibrium, the accepted contraction will take place.
      It is evident that this hypothesis confuses our notions of solids. The invariability of certain bodies, when we transfer them from one place to another, when we change their direction or their speed, gives us the experimental definition of distance and of other geometric magnitudes. The bodies that we use, necessarily participating in the motion of the earth, will always have an infinity of movements and rotations. which change their dimensions and since we don't have any way to precisely determine the absolute motion which comes into play here. These deformations remain absolutely unknown. How do you physically define the true length of a body? Does the assertion of the reality of this contraction have any sense? It results, from the researches of Einstein, to which we return later on, that the answer is negative.
      The question of stability brings forth a second objection. (Oeuvres 362) A system of electric charges, subject only to electrostatic forces, is never in stable equilibrium. This is evident when the sole restriction imposed is the conservation of electricity. In changing all the dimensions of the system by the ratio of 1 to 1+ , the charges of elements of corresponding volume being equal, we will have performed a deformation compatible with the conditions of the system. The energy will fall to of its original value. The equilibrium, therefore, is not stable. The sphere, for example, is for a

Annales 199

deformable electron a shape of unstable equilibrium, and its the same if we suppose, with Bucherer and Langevin, that its volume is invariable(1) a fortiori, whereas in Lorentz's hypothesis this restriction doesn't exist. To obtain a solid body, we therefore need to add forces of a very different character from those of electrostatic forces, or of liaisons other than incompressibility, or finally of whirling motions giving a dynamic equilibrium. But in all of these cases, Lorentz's explanation no longer applies so this explanation doesn't seem acceptable.
      Poincaré has finally objected to the hypothesis as being incomplete. New experiments could bring new terms into evidence and we would require new hypotheses if, as expected, results are negative. The question of the complete elimination of absolute motion was therefore posed and was addressed by Lorentz(2), Poincaré(3), and Einstein(4).
      It is no longer permissible to overlook the difference between "local time" and "true time", which was an essential point when we were content to explain the negative results observed up until now and a few others analogous. For us to render a full account, lets consider two points A and B which move with a constant absolute velocity v in the direction AB. A luminous wave, starting from A at instant t, will arrive (Oeuvres 363) at B at instant t'. It will have to travel

---

      (1) This is what Ehrenfest pointed out ( Physik. Zeitschr., vol. 7, 1906, p. 302): for gravitation the equilibrium would be stable; but in changing the attractions into repulsions, the energy changes sign and the equilibrium becomes unstable.
      (2) Amsterdam Proceedings, 1903-1904, p. 809.
      (3) Comptes rendus, vol.. CXL, 1905, p. 1504.
      (4) Ann. der Physik, vol. XVII, 1905, p. 891.

Annales 200

the distance AB + (t - t')v: with the speed c we have then     [That's probably AB + (t'- t)v.]

      The duration of transmission will depend on v, and its changes include a first order term -AB v/c, the correction (including higher order terms) being precisely the one we have to apply to the true time to get the local time. Lorentz(1) showed that for terrestrial phenomena, this correction is without influence. In particular, to determine the speed of light directly, we are obliged to make it cover a closed path which brings it back to its starting point; thus eliminating the first order terms. So, in the example considered, if the wave emitted at A is reflected at B, it will arrive at A after a time

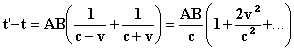
      But it will be otherwise for astronomical Phenomena. In the determination of the speed of light by the occultations of satellites, we don't use a closed path, thus, the perturbation, that the hypothesis of a translation of the solar system with respect to the ether would cause in the observed retardation, would be of a first order and of observable magnitude.
      Indeed, the delay of an occultation can reach d/c (where d is the diameter of the terrestrial orbit), or about 1000 seconds. An absolute speed of the solar system (having no connection with the system's motion with respect to the closer fixed stars)

---

      (1) Versuche einer Theorie, etc., p. 82 and following,

Annales 201

equal to 30 km per second in the plane of the ecliptic would bring about a correction of about second for the maximum observed delay, a correction which would change sign according to the relative position of the Earth and the satellite in relation to the direction of translation The systematic differences for a (Oeuvres 364) long system of observations can then reach 0.2 second, a quantity which is on the order of those which we observe in astronomy
      If, therefore, we do not wish to admit that the speed of light depends on that of the bodies emitting it and is purely relative, like all speeds (and the ether concept, alone, prevents drawing out of the relativity principle this so natural consequence), we will have to modify the definition of time.
      Lorentz has enunciated the hypotheses which would allow giving to the equations for an entrained system, as well as for the axes of coordinates, in a uniform motion of translation v parallel to the x axis, the same form as for the case of rest. He admits that all the masses are functions of velocity, thus abandoning the principle of the conservation of mass(2). We must also, as we formerly revealed, suppress the notion of solid bodies and

---

      (1) Supposing that the laws of gravitation are modified by motion as the laws of electrodynamics are, the corrections would be only of the second order and could not cancel the first order term,
      (2) The word mass, in the theories of Lorentz, Poincaré, and Einstein, has no precise meaning anymore. The number representing it depends on the motion of the system of coordinates, the motion being absolutely arbitrary. But the force depends also on this motion and it is not the second member of the equation

but (it is) their relation that alone remains invariable when we change this motion.

Annales 202

introduce a new definition of time. It will be the variable

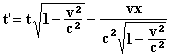
which will play the role of time in the equations.
      Time, thus defined doesn't satisfy almost any of the axioms assigned to the notion of time in the ordinary sense. Two events, simultaneous for an observer A, but taking place at different points, are not simultaneous anymore for a second observer B [who is] in motion with respect to the first. Simultaneity becomes a relative notion.
      Two equal times for observer A will not be so for B.

      The parallelogram rule for velocities is only approximated: thus for v and v' being the speeds of two bodies which are moving in opposite directions in relation to a primary system of coordinates, the relative speed of the first body with respect to the second, i.e., the velocity that an observer traveling along with the second body would observe, is not v - v', but

and it will remain steadfastly inferior to the speed of light. For two beta rays emitted in opposite directions by a grain of radium, each with a speed of 250,000 km per second, the relative speed will not be 500,000 km per second, but 294,000 km per second. The words "speed", "time", etc., have therefore acquired a significance very different from that which they normally have, and now have only a relative sense.

Annales 203

      The ether in this new Kinematics will not play any role because it no longer furnishes a system of absolute coordinates. But this concept will oblige us to replace the simple axioms of the conservation of mass, the invariability of solids, the parallelogram of velocities, etc., axioms which we should abandon only as a last resort, with complicated relationships presenting considerable difficulties to the imagination (similar to those of curved space in three dimensions), and which we generally can't treat rigorously, except by analytical considerations. We must add that this theory was presented by Lorentz with all reservations.
      Einstein ( loc. cit.) has presented the same results in a different form. He admits, a priori, for the speed of light, a law which by its nature involves a large amount of arbitrariness; the comparison with that which we will adopt in the Second Part of this work will demonstrate this sufficiently. It leads, with the principle of relativity, to a definition of the simultaneity of two events at two different points, of which he makes a relative notion, and more generally leads to the new Kinematics which has just been discussed. The simultaneity included in the (Oeuvres 366) definition of the length of a body in motion in relation to the fixed marks of a standard measure (since it will be a matter of pointing simultaneously to the two extremities of the body. otherwise the body would move during the interval) this body will appear to be of a different length to an observer at rest, according to its more or less large speed (although its true length remains invariable). We therefore avoid the contractions admitted by Lorentz, or rather we see that their reality is only a question of definition.
      Einstein verifies that Lorentz's equations are

Annales 204

thus made Independent of absolute motion, and that the law admitted by him for the propagation of light is in accordance with the equations. These then, in the measure that they express this law of propagation, become superfluous; moreover, the reasoning does not demonstrate at all, as some authors have believed, that these transformations are the only group which leaves Lorentz's equations invariable. This problem has rather to do with Poincaré's methods (loc. cit.).
      Bucherer(1) was led, by considerations on the relativity of motions to abandon the notion of ether. Lorentz's equations should always be applied by assuming that the system of coordinates is at rest with respect to the point P whose motion we study. Bucherer only considers the case of uniform motions; the action on an electron propelled with a relative velocity u = v' - v in relation to P, according to formula (13) (where we set v' = u, v = 0), will be given by the formula

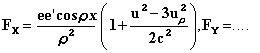
      For two closed currents, we verify easily ( see the Second Part) that only the terms proportional to vv' play a role, with the accelerations excluded, which we haven't taken into consideration, and terms in . It is moreover what should happen if the intensity of the force is proportional to the product of the intensities of the currents. The action of two elements of current on each other will from then on be

      The hypotheses of Ampere are verified. The action is

---

      (1) Physik. Zeitschr., vol. 7, 1906, p. 553.

Annales 205

parallel to the line of junction of the elements; but the parenthesis should be

      Bucherer's hypothesis is therefore irreconcilable with the laws of closed currents.
      This is because the notion of field ceases to be applicable there.
      We are therefore brought back to the complicated hypotheses which were set forth. We must say, in closing, that these complications occur not only at great speeds, but also in Fizeau's experiment on the entrainment of waves, for example. In effect, according to the principle of relativity, an observer carried along in the translational movement of a transparent body will find, for the speed of propagation of waves in this environment, the same value as if he were at rest (supposing the period to be the same, or the dispersion negligible). We would conclude that, in ordinary kinematics, the waves are totally carried along by the substance. There is nothing to it. The term velocityhas a new meaning, and in reality, Lorentz's proof continues to be applicable; we come back to Fresnel's coefficient.