We know that the introduction of the notion of force into mechanics was the subject of much criticism. This notion calls for muscular sense, whereas the ideas of space and time are primarily of tactile and visual origin: and the irreducible psychological duality introduced at the very base of this fundamental science leaves a certain discomfort in the mind, justifiably so, for it seems very obvious that the notion eliminates itself in each particular case. Whether we measure the forces by masses and accelerations, or by electric deformations, whether we oppose their effects with those of gravity, etc., what we really observe and measure is always a displacement, or in the absence of a displacement; again, in this latter case, we only end up defining the difference of two forces. In the equations of Mechanics, as applied to any particular example, there remain only the relations of space and time, with certain coefficients properly chosen and invariable which are the masses or other physical constants. With

Annales 160

regard to pure logic, it is therefore with good reason that many experts have rejected the introduction of the notion of forces in the fundamental expressions as being useless.
      Modern electrodynamics is entirely based on the notion of electric and magnetic forces. If this were absolutely necessary it would be regrettable. But it isn't so: these notions eliminate themselves in the equations, they are logically useless. In the final analysis the theory only expresses the existence of certain relations of time and space, as it is in the case of Mechanics. It will therefore be preferable to express these relations directly; we thus come back to the classical elementary actions.
      In fact, what are the exact definitions of the vectors for E and H fields? I say that these vectors are defined by the theory itself. Thus, without knowing the significance of these symbols, we can at once, by means of certain hypotheses that (Oeuvres 330) we will examine in the next section, integrate the fundamental equations by the method of retarded potentials, and we will be led to expressions (XIV) and (XVI). The equations of motion for a material point of charge e, of mass m and of coordinates x_ı, y_ı, z_ı will be

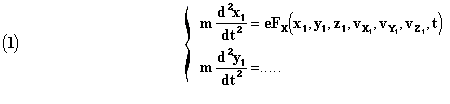
      If we desire to take into account the action of the electron on itself, or of liaison, d'Alembert's principle has to be applied, and we have, in extending the integration over the whole of the electron, and designating by virtual displacements compatible with the liaisons, by

Annales 161

the densities of the substance and of electricity,

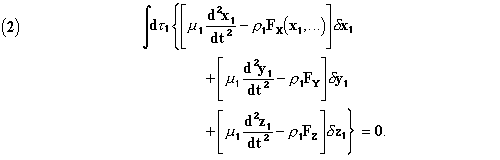
      After having replaced F_x, . . . with the value (XIV) or (XVI) (the terms solely relative to the electron will play a special róle. We will have in (1) and (2) only relations of space and time, even when μ = 0, that is to say, when the mass is entirely of electromagnetic origin.
      Now, I say that Lorentz's equations don't effectively express anything more than (1) and (2). That is to say that the field never plays a róle in pure ether. In fact, we can only determine the field's magnitude and direction by placing a body and observing the mechanical forces that it feels or rather its motions and those of the ions in its near vicinity, motions which are indicated by luminous, thermal, chemical, etc., phenomena. Therefore, we only know F, and that, only in points of x₁, y₁, z₁ where there is electrified matter, and we deduce E and H by reasoning (which is not always so simple when we have to consider absolute motion). This is to say that, in all cases, to know the (Oeuvres 331) formula that gives F as the result of elementary actions exerted by an element of charge on another element of charge, and that this second representation, with regard to the facts, is exactly equivalent to the first one, which is based on the field and its partial differential equations which only play a purely mathematical róle. We can, if we please, get along

Annales 162

without the notion of electric and magnetic fields.
      It is important to specify the sense of this affirmation. In the theory of light, for example, everything thus represented with regard to Lorentz's theory can be derived from elementary actions between ions in the luminous source, the ones in the dielectrics or conductors which constitute the optical display, and finally the ones in the retina or photographic plate which receives the impression. Thus, we are accustomed, for example, to describe the phenomena of diffraction that we observe in the case of a slit used with a screen by considering with Fresnel that the points of ether situated in the slit as so many centers of disturbance. This does not conform to the equation for retarded potentials though. Electric charges are the only points of origin for waves. Lorentz's theory, or the law of elementary actions, will explain it as the combined action of ions in the source and in the screen; besides, it is easy to show, using Huygen's principle as Kirchoff has it, the equivalence of the two methods with regard to results.
      It wouldn't be allowed any longer to say that the field is a purely mathematical intermediate which we could do without, if it were possible to perceive its existence in a region of ether without placing any matter in the region. That is what would have happened, for example, if ether, under the influence of a field, were to be susceptible to modification or were to move itself more or less as Hertz wants it to, and as Lord Kelvin demands.(1) Interference experiments would have put this speed into evidence. These ideas were generally very widespread;

---

      (1) Lord Kelvin, Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light, London, 1904, p. 159: "It is absolutely certain that there is a definite dynamical theory for waves of light, to be enriched, not abolished, by electromagnetic theory."

Annales 163

but we know that (Oeuvres 332) the experiment, conducted several times,(1) gave only negative results, as do all the experiments designed to prove the existence of ether. The hypothesis of all these motions, on the other hand, has not lent itself to any plausible mechanical explanation of electrical actions in their effects. Lorentz was therefore led to exclude it in the recent statements of his theory; and that is what gives the go-ahead for us to eliminate the notions of force and field in this theory without touching any fact of reality or any possible experiment according to it.
      Lorentz has already indicated(2) this point of view: "We therefore see, in the new way I'm going to present it, Maxwell's theory draws nearer to the older ideas. We can even, after we have established the simple formulae that describe the motions of the particles, leave out the reasoning that spawned them and consider looking at these formulae as expressing a fundamental law comparable with those of Weber and Clausius." The actions, however, are not instantaneous anymore; and we have seen, in the light of this important restriction, that there is even an identity with Clausius' law.
      We can easily see that the notion of field introduces the notion of absolute motion as soon as the velocities come into play, either in the field expressions or in the expression for its action on bodies. It isn't likely anymore that it depends only on coordinates and accelerations.

---

      (1) See in particular O. LODGE, Phil. Trans., Vol. CLXXXIV, 1893; HENDERSON and HENRY, Phil. Mag., 5th Series, Vol. XLIV, 1897, p. 20.
      (2) Arch. neerl., Vol. XXV, 1892, p. 433.