Now I intend to examine more closely the hypothesis which relates differential equations

Annales 164

(IX) and (X) to retarded potentials formulas (XII) and (XIII) and to show that the transformation of the latter ones from the first ones is immediate, but that the inverse proposition is far from being true.
      First we have to recognize the fundamental importance of the formulas. In contrast to mechanical phenomena, (Oeuvres 333) electromagnetic phenomena are, in general, irreversible because of radiation. We can, by this motive, even hope to get by their means a more complete interpretation of irreversible physical phenomena. But Lorentz's equations don't change when we change the direction of time. They contain the affirmation of reversibility, whereas for retarded potentials and elementary actions, the positive and negative directions of time play entirely different rôles. We insert, as in Helmholtz's irreversible cycles, a speed which is hypothetically impossible to change the sense, the speed with which waves constantly move away from the bodies that generated them. It is from this, that electromagnetic irreversibility is derived. This additional hypothesis which precedes must therefore be examined with care.
      With f(x,y,z,t) a continuous function, proportional to the electric density ρ(x,y,z,t) and ϕ another function having the property of continuity of potential in all space and at infinity and satisfying everywhere the equation

it is easy to verify that the integral

Annales 165

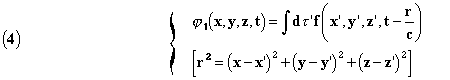
is a solution of (3). In fact, lets isolate a small volume τ_o around point xyz. We'll be able to differentiate the integral under the summation sign relative to the rest of space for which xyz is an external point. In applying the operation
(1/c²)(∂²/∂t²) - Δ, we find zero. Inside τ_o the ∂²/∂t² operation is performed again, under the summation sign, and gives a result closing to zero with τ_o. To do the Δ operation lets put r, being very small, into τ_o.

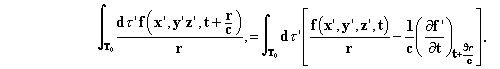
      The -Δ operation applied to the first term gives 4πf(x,y,z,t) according to Poisson's theorem. In the second term the denominator r is missing. The result closes to zero with τ_o. We therefore obtain equation (3). I don't insist on the condition of continuity lightly, in that we have to insure that there are derivatives of f.
      We demonstrate that

and, more generally,

are solutions of (3), provided that the arbitrary functions and satisfy the relation
     

Annales 166

      The solution φ₁ corresponds to waves which move away in all directions from the electric charges that generated them; φ₂ is for waves coming from infinity converging on the same points. In contrast to φ₁, which depends only on previous states, φ₂ depends on subsequent states. The solution φ₃ contains both kinds of waves. And finally, φ₄ corresponds to waves whose centers of disturbance may be located in pure ether, where f = 0. Experience shows, and Lorentz admits, that only φ₁ waves can exist, and besides, we will see that contrary hypotheses would involve inadmissible consequences, such as the possibility of perpetual motion. We conclude, to begin with, that Lorentz's equations (and the result extends to those of Maxwell and Hertz) accept an infinite number of solutions, satisfying all conditions, but incompatible with experiment.
      We readily find such solutions, and are led to set them aside a priori, each time we calculate, for example, the electrical oscillations (Oeuves 335) of a system (a conducting sphere, Hertz's excitor, an oscillating electron, etc.).
      Let's discuss the hypothesis by which we believe we can eliminate these solutions. We show that we have for all solutions of (3) inside a closed surface S

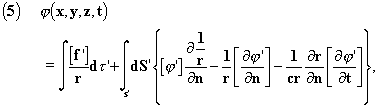
where we have set, as before,

      Suppose that at any instant t=0 situated

Annales 167

in the past we had everywhere, or at least at great distances, ϕ = 0, ∂ϕ/∂t = 0; we could, for all positive values of t and at all points xyz, choose for S a sphere of center xyz and radius R > ct big enough so that all terms of the surface integral will be zero. Formula (4) will remain. This reasoning calls for the following remarks:
      1° The terms for uniform translational or rotational motion which enter into electromagnetic theory never satisfy the relative conditions at t = 0. This theory therefore remains excluded. More generally, the authors who have used this reasoning, once the formula was set up, didn't bother to verify in the equations they dealt with if this condition is fulfilled. It isn't in most cases. Now we have seen that the formula must be absolutely general.
      2° If for t = 0 there is only a very weak field at very great distances, this field, if it is for a convergent wave, could acquire a few moments later a great intensity at a given point in space. It is not sufficient therefore to suppose a weak field for the moment t = 0 for all space (or at least at great distances). It has to be rigorously zero (which is an hypothesis of inadmissible character in physics) or that had been previously excluded in the convergent waves, which would be a petition of principle. In the case of sound (and this analogy can (Oeuvres 336) mislead easily) friction destroys the wave entirely after a few moments, and the reasoning is practically the same. It is not the same though for ether and we should expect, a priori, to find a similar state of affairs to the one we observe at seaside, where in addition to the divergent waves produced by solid bodies of the shore, there are others

Annales 168

which constantly come in from the sea and are not produced by solid bodies. So if formula (4) is not rigorous, we would have to expect at each moment the sudden creation of an intense field, a kind of electromagnetic wave coming from infinity or which diverges from a region of ether through which it just converged.
      3° Only solar and stellar radiation, which has been creating an oscillating electromagnetic field throughout the universe daily for an extremely long time, could oblige moving the instant t = 0 back beyond all limits of cognizance. A hypothesis so fundamental must not present this inadmissible character.
      4° Lets examine what must have happened before the moment t = 0. We will find, in changing c into -c, the analogous formula

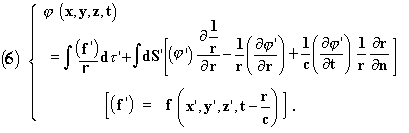
      The same reasoning will give

Annales 169

but, after a short time, the system is at a new state (Oeuvres 337) of rest. It is not exactly at rest, any more than it was before the experiment. It is in that state only sensibly. If we begin our reasoning during the first state of rest, there would only be converging waves. Why do we choose the first state of rest but have no inclination for doing a new experiment wherein the second state of rest plays the same role as in the first? It is because the elements away from the immediate area, which are inaccessible to the experiment, play a preponderant role in the hypothesis. If they were to send us convergent waves, our approximate, based on the close-in elements, would soon cease to give an approximation, even a coarse one.
      Fortunately, we know, a priori, by means of a lengthy experiment, that the distant waves diverge. This is what allows us to ignore them and also renders the demonstration unnecessary. If ether had viscosity, similar to that of air, very different considerations would ensue and there wouldn't be any reason to be surprised by irreversibility, since we would have introduced it in the equations themselves.
      More generally, any theory which makes more specialized hypotheses about the initial state than the law of potentials requires, will not be admissible. It would exclude some actual phenomena and would allow, for t < 0, impossible solutions. Therefore, what are the initial conditions, necessary and sufficient, for (4) to hold?
      Let's postulate
                  φ = φ₁ + ψ
      We will have
 
in all space; and ψ = 0 at infinity. For ψ to be constantly nil, it is necessary and sufficient that for t = 0 we have

Annales 170

Ψ = 0, ∂ψ/∂t = 0 in all space. This says that for formula (4) to be applicable over all time, it is necessary and sufficient that it hold for two instants, t = 0, and t = dt infinitely close, a statement about which there is evidently nothing to be drawn from Maxwell's point of view.
      Can we replace the initial state hypothesis by some other equivalent general condition?

      Lorentz(1) doesn't make use of the hypothesis. He simply admits that the surface integral in (5) is nil when S moves away indefinitely. After having written (4), he continues, "This solution is not therefore the general integral of (3). There will also be, for example, solutions corresponding to a movement of waves which would be directed towards the element of volume instead of moving away from it. We will reject them from the theory by admitting, once and for all, that charged elements are the only points of origin for disturbances. We exclude also the states of ether which are completely independent of the charged substance; which if non-existent, the ether would remain continually at rest."
      But let's apply these ideas, without change, to formula (6). As the surface integral vanishes we will get convergent waves. But neither method of proceeding is admissible. These surface integrals, considered as functions of x,y,z,t, are general solutions of (6). They would not therefore approach zero for a given value of x,y,z,t when the surface moves away indefinitely. They have an invariable value, finite or nil, according to whether the chosen

---

      (1)Elektronetheorie, p 158; see also WIECHERT, Arch. neerl., 1900, p 549, and P. HERTZ, Untersuchungen uber unstetige Bervegunen eins Elektrons, Inau. Diss., Gottinge, 1904, p 5 and 12, and note. In his first thesis of 1892 Lorentz contented himself with verifying that satisfactory equations exist.

Annales 171

solution is finite or nil. There is nothing to draw from such identities. Finally, there is no precise sense to attach to this proposition; the disturbances that are dependent on ether are the only ones to be excluded. If we could use, a priori, formula φ₂ or φ₃, which depend only on the material, we could write

      The inadequacy of these statements, and others analogous, is that they hold that, the decomposition of a field of waves is a mathematical operation which can be done in an infinite number of ways. But the character of this operation is doubly artificial from the viewpoint of Maxwell's ideas because consideration of the origin of the waves demands consideration of the entire field during a finite interval of time, whereas Maxwell saw an essential advantage in his theory, precisely from the fact that it makes it unnecessary to consider elementary actions and the field's origin and only concerns itself with the immediate surroundings of the point under consideration. We see that these statements are useless, and that to eliminate the physically impossible solutions it only requires adoption a priori the formulae for retarded potentials which distinguish elementary actions like the classical theories did, and to prove that they satisfy the equations is to say that they can replace them completely, whereas the inverse is not the case.

Annales 172

      In bringing these results closer to the ones in the preceding section, we see that in the last analysis it is the formula of elementary actions, and not the system of partial differential equations, which is the complete and exact expression of Lorentz's theory.
      We have to add the hypothesis of absolute coordinates. We have just seen that ether, instead of playing an independent role, and even preponderant, as we should have expected, since it is supposed to be the reservoir of all electromagnetic energy, steals away once more. Its only role will consist in providing, though contradicting experience, a system of absolute coordinates.
      We will evidently have the same difficulties in passing from any kind of system of partial differential equations, reversible at least wherein it concerns pure ether, to irreversible solutions that the experiment demands. In Hertz's theory, even this seems impossible. The partial differential equations and the notion of ether are essentially inappropriate to express the comprehensive laws for the propagation of electrodynamic actions.