We know that Maxwell did not work on hypotheses on the nature of electric currents. Lorentz claims that all conduction current results from motion of electric particles, which are subjected to a kind of friction in conductors and to elastic forces in dielectrics. Many experiments have, in the last years, confirmed this hypothesis. This concept has permitted Lorentz to consider only the dielectric ether in his fundamental equations. Renouncing a purely mechanical explanation and the impenetrability of matter, Lorentz considers the ether as immobile and even present in the interior

---

      (1) H.A. LORENTZ, Archives neerl., t. XXV, 1892; Versuch einer Theorie der elektrischen und optischen Erscheninungen in bewegten Körpern, Leiden, 1895; Elektronentheorie: Enzyklopädie der math, Wissenschaften. Bd. V, Heft l, Leipzig, 1904--POINCARÉ, Électricité et Optique, Chap, III, p. 422.

Annales 153

of ions and electrons. The ions and electrons modify it physically, and this modification, which is difficult to picture in a concrete fashion, is characterized by two vectors; the electric or dielectric displacement vector E, whose components are E_x, E_y, E_z, and the magnetic vector H (H_x, H_y, H_z). The electric charges are fixed to the ions which are considered undeformable. Where the electric density, "ρ" is measured in electrostatic units at xyz, at time t, the system of coordinates being connected to the stable ether, and v the velocity of the electric substance in (x ,y, z, t) and c, the speed of light; we have, for these constraints, the system of equations

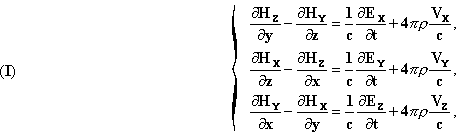
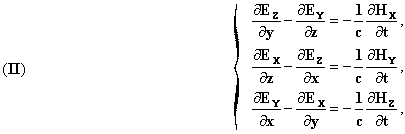
The field therefore created in the ether by other charges present, exerts on the element of charge ρ dτ the mechanical force represented in magnitude and direction by the

Annales 154

vector F ρ dτ where

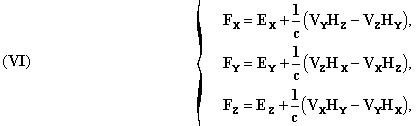
In this theory there is no magnetism: the magnetization comes from Amperian particle currents.
      By means of certain hypotheses, to which we will return, this system of equations integrates itself by the introduction of retarded potentials. As a matter of fact we show that all solutions of the system (I) to (V), where we assume the data ρ, V_x, V_y, V_z can be expressed in the form

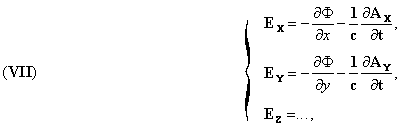
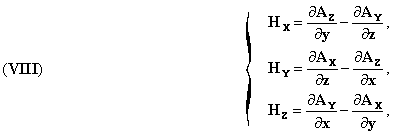
the functions Φ (scalar potential) and Ax, Ay, Az (components of the vector potential) being continuous with their first derivatives in all space, from zero to infinity, and satisfying the equations

Annales 155

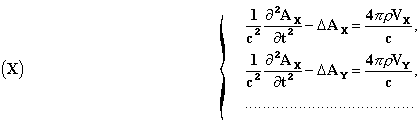
and

Lorentz satisfies these conditions by setting

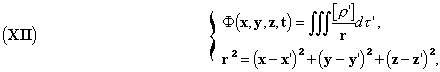
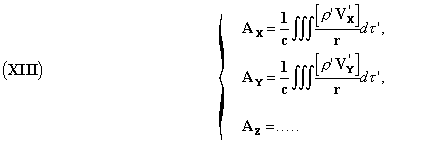
These expressions have the form of Newtonian potentials, with the difference that instead of taking the value of ρ at point x'y'z' at time t, we have to take it at the previous time t' = t - r/c, the time r/c being necessary because of the propagation; this is what we will point out along with Lorentz by the notation

The field is therefore completely determined, and in introducing the expressions (XII) and (XIII) into formulae (VII), (VIII) (Oeuvres 326) and (VI), we obtain for F_x

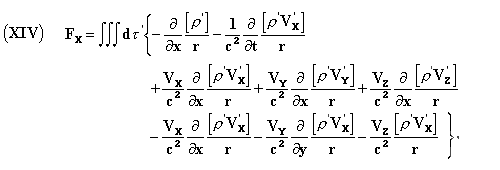
and similar expressions for F_y, F_z. In introducing

Annales 156

the total derivative

and setting

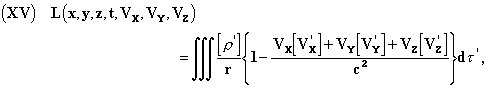
Schwarzschild(1) has found for F_x the remarkable form

This is the form of Lagrange's equations. The expressions (XIV) and (XVI) give the force undergone by an electric point of unit charge, expressed by means of elementary actions analogous to the ones considered in the old electrodynamics, without the notion of non-instantaneous transmission that we find again in Gauss and C. Neumann. A charge e', sensibly point-like, exercises, under very general considerations, on another similar charge e, a force

(Oeuvres 327) where

---

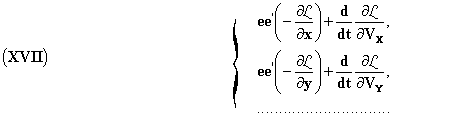
      (1)Gottinger Nach., Math.-Phys. Klasse, 1903, p.126.

Annales 157

This expression reduces itself, to a first approximation, to the law of distance squared. We can therefore name it the generalized Newton's law. The explicit expression will be given later on.
      In these formulae the notion of field doesn't come into play. It is very remarkable that Clausius, like Weber, in seeking to account for the electrodynamic actions, by means of actions at a distance, depending on positions, velocities and accelerations of the electric points, has derived the same formulae (XV) and (XVI), with the only difference that the actions are instantaneous, so that we have to take the values of ρ' and v' at time t and not at time t-r/c.
      This very remarkable result, due to Schwarzschild, shows that Lorentz's theory is very close to the old theories.
      The first form that Lorentz gave to his theory was less abstract in the sense that, following the path that Maxwell laid out, he started from Lagrange's equations, introducing two kinds of variables, the first ones determining the positions of the electrified particles, the others the state of the ether. We attribute to this latter one kinetic energy, without determining its internal motions. It suffices that they exist. Hamilton's principle permits, likewise, restricting the variations under certain conditions, to obtain the fundamental equations (I) to (VI) by considering the electrical energy...

as potential energy, and magnetic energy

Annales 158 (Oeuvres 328)

as kinetic energy.(1) This deduction is fairly complicated and can be done in various forms.(2)
      These two aspects of Lorentz's theory are clearly distinct. The second one is similar to Larmor's theory,(3) which, in leading to the same formulae offers precise hypotheses on the motions of ether in an electromagnetic field as borrowed from Lord Kelvin's conceptions on gyrostatic ether. Ether is incompressible and moves itself in the direction of magnetic force lines.
      We know that Maxwell and Hertz explain the mechanical forces that a substances experiences in an electromagnetic field by the pressure that ether is supposed to exert on the substance, and conversely: the action of one is equal and opposite to the reaction of the other in all respects. These pressures, as Helmholtz has shown,(4) tend to set the ether (supposedly incompressible) in motion; they are, by unit volume, proportional to the time derivative of Poynting's radiant vector S:

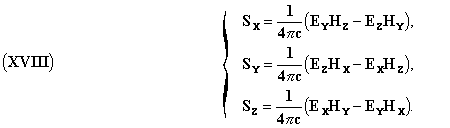
Lorentz considers ether as immobile; he is therefore inclined to Maxwell's theory of pressures

---

      (1) LORENTZ, Proc. Amsterdam Acad., 1903, p. 608; Elektronen-theorie, p. 165 to 170.
      (2) LARMOR, Aether and Matter, Cambridge, 1903, Chap. IV. -- SCHWARZSCHILD, Göttinger Nachr. 1903, p. 125.
      (3) LARMOR, Proc. Roy. Soc., Vol. LIV, 1893, p. 438; Aether and Matter.
      (4) Gesammelte Abhandlungen, Vol. III, p. 526.

Annales 159

and, by that, the equality of action and reaction, the non-compensated force being characterized by the vector (1)

Let's observe, in concluding this brief exposition, that if we admit unknown motions in ether, the solution of the equations is determinable only for quantities close to the order of the speed of the ether divided by that of light. (Oeuvres 329)

---

      (1) POINCARÉ Électricité et Optique, p. 448.