On the Question of the Constancy of the Speed of Light

by Erwin Freundlich

An English translation of

Zur Frage der Konstanz der Lichtgeschwindigkeit

Physik. Zeitschr. 14, 835-838 (1913)

Translation by Julie Newton. Final smoothing by R.S. Fritzius (in progress).

Installed as a web page on 11 Jul 2011. Latest update, 03 Nov 2011.

The question of whether the speed of light is dependent on the movement of the light source is of such interest to the view of modern physics, that “an astronomical proof of the constant speed of light,” such as seen in the article from Mr. W. de Sitter[1] published in this journal, would be of extraordinary importance.  Because I immediately became uncertain as to whether the current facts permit such an absolute conclusion, I undertook a more exact discussion[2] of such and reached the conclusion that in my opinion, no such “proof” can be enunciated.

Mr. de Sitter examines the influence that the emission theory assumption, that the speed of light in any direction equals the sum of the speed of the light source in the same direction plus the speed of light of stationary light sources, would have on the apparent motion of spectroscopic binary stars, and finds that their motion could not be Keplerian and that it would become evident that the time interval between two digressions [side-to-side excursions] would in one instance amount to [* - See diagram at end.], and at another time, it would be where T designates the half  period of the system, Δ the distance to the system, u the speed of the bright component in its orbit and c the speed of light in its usual sense.  Because the size  can by all means reach the order of magnitude of T, the midpoint of the cycle can shrink to zero when

 

and can even become negative beyond that. This odd occurrence has never been observed, therefore Mr. de Sitter draws the conclusion that the speed of light would have to be independent of the movement of the light source.

In fact, the conclusion made by Mr. de Sitter is without a doubt strong, if one uses emission theory in its unaltered state as a foundation; that is, if one assumes that the only possible effect of a light source’s motion is a complete addition of its speed to the speed of light which would [otherwise] be proceeding from a stationary light source, because, for the case that Mr. de Sitter cites, and the case in which the distance Δ is assumed to be very small, the extreme instance will be reached.   It therefore would be idle to assume that the addition of

the two speeds goes against another law as long as one has no physical interpretation for the same, and if the appearances of the spectroscopic binary star make themselves obviously apparent.  This points to a certain dependency of the speed of light that has so far remained unexplained.

Mr. de Sitter’s argument that the measured shift in the lines of a spectroscopic binary star cannot be interpreted by Keplerian motion if the speed of light were to be variable does not apply to the entire field of possible movements, because the orbital movement with a variable speed of light, as Mr. de Sitter views it, is primarily identical to the Keplerian orbital motion of an ellipse, whose line of apsides is directed towards us, while the periastron lies on the side pointed away from us.  The speed in the direction of the line of sight, as it is measured in spectroscopic observations, is in the first case

 

and in the second case

 

in which l means the longitude of the orbit, e the eccentricity of the Keplerian ellipse and ω the longitude of the nodes, in our case = 90º.  In contrast, the constant k represents the influence of a variable speed of light on the apparent motion [of the star] and, in the case of Mr. de Sitter, [it] has the value of

  (μ=daily movement),

 

whereas we want to make it to be

 

where the proportionality factor x dictates that the speed of the light source does not assume its full magnitude in the [combined] speed of light; rather x is so small, that for the distance range which our known binary stars sweep through, the size

<2

 

remains. Under these restrictions our above assertion that both forms of movement agree to the first order is valid, if one disregards the higher powers of eccentricity.  Mr. P. Guthnick drew the two commensurate speed curves for e=0.25 and k=0.5 (see figure), in which he assumed a value of 100 km/sec for u.  I did the same still for e=0.5 and u=45 km/sec because the latter value for u complies with the approximate average of the orbital speeds of the systems known to us, and it occurred to me to determine the approximate boundary for e, at which both motion phenomena deviate strongly enough from each other to attract the attention of the observer.  In the first

 

 

 

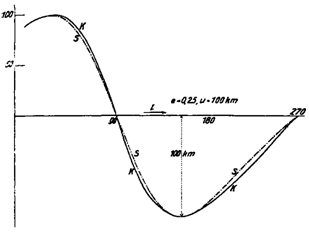
instance, e=0.25, u=100 km/sec, the values of ρ deviate at most only 6 km/sec from each other, so that it is difficult to differentiate the two forms of motion for the very unclearly defined paths of most spectra; for e=0.5 and u=45 km/sec, the deviations climb up to 10 km/sec.  One can surely get better consistency with a careful compensation; one must consider that the observer seeks in his best estimate to set his trajectories so that they can only be Keplerian ellipses.  Thus one’s observances will best be presented, and if one searches through the catalog of spectroscopic binary stars by W.W. Campbell[3], he finds that various observers of the same systems rightly arrive at different orbital elements. 

In any case we can say that for all orbits whose eccentricities amount to smaller than 0.5, it may not always be simple to separate the two forms of movement discussed above, and thus to judge whether the eccentricity given is real or spurious, especially as the systematic anomalies of both curves exhibit a regularity that could be considered legitimate  I will return to this later.

Now, it could be that a certain percentage of these smaller eccentricities is more obvious because larger eccentricities with Keplerian motion are, in general, less common than smaller, although nothing in and of itself suggests why such spurious eccentricities should be, for example, smaller than 0.5 rather than larger than 0.5; if we don’t want to assert the limit here through the size of variable x,  then a larger percentage with only spurious eccentricities would have to  be among the orbits with larger eccentricities.  If the divergence of both motion phenomena should escape the observers, which could be determined  with the assistance of the materials, (which I am currently not able to do) then it would have to be clear that only these spurious ellipses appear to be oriented relative to us in a very certain manner:  It would have to be as I mentioned in the beginning, the line of apsides is directed towards us and the periastren lie on the side facing away from us, while the location of the line of apsides and the periastren for the real Keplerian orbits would have to be distributed by chance.  Here is where the strongest doubts arise regarding Mr. de Sitter’s conclusion.  It has in fact been known for a few years that this appearance is able to be observed in quite obvious ways, causing Mr. Miller Bar[4] for example to raise concerns as to whether the measured shifts in curve actually point to real motion in a Keplerian ellipse because it would be almost unimaginable that almost all of these ellipses (23 systems among 28 that he takes as his basis) appear relative to the observer in a certain manner. Especially the systems with large eccentricities show these unique phenomena so remarkably, that out of 8 systems with an eccentricity e>0.5 seven have their periastron lying on the side which is turned towards us, while this event for smaller eccentricities appear less remarkable, quite understandable since for smaller values of e the location of the periastron can become less exact and at the same time real eccentricities would have to be a relatively larger portion.

There is a further argument I would like to raise.  The systematic variations between the speed curves of both motion phenomena show regular cycles with amounts of T/2, T/3…, in which T is the period, and experience has taught that remainders (?) with such cycles usually assert themselves more obviously/remarkably.  This can be explained by an assumption of a third disturbing body with suitable cycle in the system in question; a way out that naturally arouses suspicion.  The orientation of the line of apsides and periastren relative to the observer is the most difficult to understand up to this point, and this would be readily explained by an independence of the speed of light from the movement of the light source; likewise the recurring remainders of certain cycles.  These are in no way definitive criterion against the constancy of the speed of light, as long as we have no interpretation for the constant x and can only state something about its order of magnitude.  Because the sun lies near the center of the Milky Way, one such legitimate trajectory orientation towards the direction of the center could be of cosmological origin; at this point we are still missing the necessary deep insight into the Milky Way’s processes of development.

In order to make a decision about the questions brought up here, one would have to examine especially opportune/advantageous spectroscopic binary stars from this angle, and exclusively such binary stars whose parallax, i.e. the distance from us, is as precisely known as possible.  As of today, we know with few exceptions the parallaxes of stars only by their orders of magnitude, and therefore the assumed values can vary by ± 100 percent or more from the actual values.  If variations from Keplerian motion are established though a more precise discussion of the observations, it would depend on whether one could exhibit these variations by way of a single value of the parameter x for possible varied values of the distance Δ.  It would also have to make the accumulation of the effect of the system noticeable with growing distance.  The spectroscopic binary stars reveal such multi-faceted relationships, for example dependence between eccentricities, cycles, spectral types etc., that are probably unrelated to our present question, and our theory also necessitates such a careful study, that we, due to our present knowledge, still cannot draw clear cut conclusions for the benefit of one of the two hypotheses—constancy or inconstancy of the speed of light.  Spectroscopic binary stars are unusually sensitive touchstones[5] for this question, and according to the methods debated above, it would possibly be a direct test of the assumption of the principle of relativity, the constant of the speed of light.  In fact remarkable symptoms are present, that hitherto can be explained by the variability of the speed of light.

Berlin, Kgi. Observatory.

 (Received 1 July 1913.)

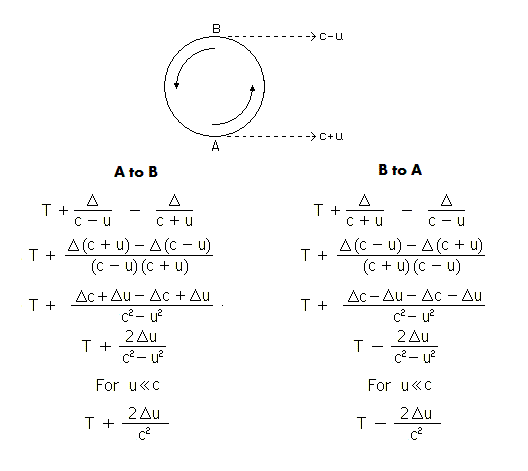
[*] Derivation of Digression Delays:  Δ = Distance to Observer  (Not in original document.)