The Barr Effect
70
THE ORBITS AND "VELOCITY CURVES" OF
SPECTRO
SCOPIC BINARIES
By J. Miller Barr
I.
In looking over the published papers on spectroscopic binaries, it will be remarked
that the "velocity curves" -- as hitherto drawn for these objects--are often unsymmetrical.
A closer examination reveals a curious general similarity in the form of
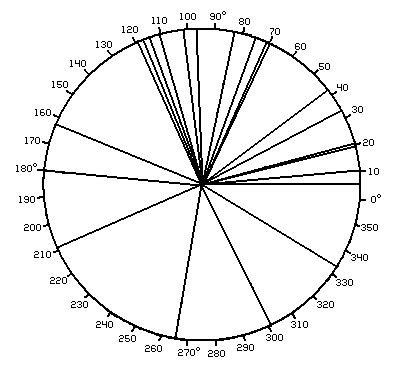
The radial lines represent the values of ω, i.e., the computed longitude of peri-
astron)), for twenty-three spectroscopic binaries. See accompanying table.
such curves--the ascending branch of the curve, with few exceptions, being of greater length than the descending branch. This fact, although of great theoretical interest, seems to have been hithero overlooked by astronomers. Its significance will be apparent from an inspection of the diagram and table given below.
Orbits and Velocity Curves of Spectroscopic Binaries 71
LIST OF SPECTROSCOPIC BINARIES
==================================================================================
: STAR P e ω K Reference
——————————————————————————————————————————————————————————————————————————————————
: d km.
α Andromedae 100.? ... [0 - 180] ... Astroph. Jour., 20, 146, 1904
{*} Polaris 3.9683 ... [0 - 180] 3.0 " " 14, 52, 1901
{#} β Arietis 107.0 0.88 19.7 32.6 " " 25, 320, 1907
Capella 104.022 0.016 117.3 25.76 " " 14, 263, 1901
η Orionis 7.9896 0.016 42 16' 144.75 " " 17, 68, 1903
δ Orionis 5.7325 0.103 33 19 100.85 " " 19, 268, 1904
ζ Tauri 138. 0.180 9 45 14.95 " " 22, 115, 1905
γ Geminorum [3.5y ?] ... [0 - 180] ... " " 22, 84, 1905
{*} ζ Geminorum 10.154 0.22 333. 13.2 " " 13, 90, 1901
α2 Geminorum 9.2188 0.503 265.35 13.56 " " 23, 351, 1906
κ Cancri 6.393 0.149 162 16 67.8 " " 25, 315, 1907
α Carinae 6.744 0.18 115.84 21.5 " " 26, 268, 1907
κ Velorum 116.65 0.19 96.23 46.5 " " 26, 271, 1907
η Virginis 71.9 0.254 180 0 26.8 " " 26, 282, 1907
{#} Mizar 20.6 0.502 101.3 142. " " 13, 324, 1901
α Draconis 51.38 0.43 19. 48. ± Jour. R.A.S.C., 1, 237, 1907
{*} X Sagittarii 7.0118 ... [0 - 180] ... Astroph. Jour., 25, 330, 1907 {1}
{*} Y Ophiuchi 17.207 0.10 209.2 8.5 " " 25, 330, 1907
{*} W Sagittarii 7.5946 0.320 70.0 19.5 " " 20, 149, 1904
μ Sagittarii 180.2 0.441 74 43 64.5 " " 26, 157, 1907
{#} χ Draconis 281.8 0.423 119.0 18.15 " " 11, 131, 1900
β Lyrae 12.908 0.07 83.4 181.05 " " 6, 328, 1897
{*} U Aquilae 7.0240 ... [0 - 180] ... " " 25, 330, 1907
η Aquilae 7.176 0.489 68.91 20.59 " " 9, 59, 1899
S Sagittae 8.3832 ... [0 - 180] ... " " 20, 231, 1904
{#} θ Aquilae 17.17 0.725 20. 52. ± Jour. R.A.S.C., 1, 357, 1907
{*} T Vulpeculae 4.4358 0.43 111. 17.6 Astroph. Jour., 25, 330, 1907
{*} δ Cephei 5.366 0.46 [0 - 180] 20.5 " " 1, 160, 1895
η Pegasi 818.0 0.155 5.61 14.20 " " 14, 202, 1901 {2}
λ Andromedae 20.546 0.086 301.0 7.07 " " 24, 345, 1906
----------------------------------------------------------------------------------
{* Cepheid variables, currently considered as pulsators (as of 2010), are marked with asterisks.}
{# Visually resolved double-lined spectroscopic binaries are marked with pound signs.}
{1 Table III in this Albrecht reference gives a period of 7.01 days. The refined value
of 7.0118 days may have been furnished via personal communication.
See Lick Obs. Bul., 5, 111, 1909}
{2 The page number was given as "20."}
Note.--The elements refer to the brighter component of each system, except in
the case of Mizar
(ζ Ursae Majoris), where the value of K is that of the relative orbit.
The table includes all stars (so far as known to the writer) for which the "velocity-curve" appears to be certainly unsymmetrical. It contains, for each star, the computed elements P, e, ω, and K, except in a few cases where such data are not available.*
* For α Andromedae and γ Geminorum only the general form of the oscillation [Continued at bottom of next page.]
72 J. Miller Barr
Of the thirty stars included in this table there are but four for which the values of ω (as calculated) lie between 180° and 360°. For these four stars we have in each case,
where D denotes the time-interval during which the star's "radial velocity" is decreasing ; I the interval during which it is increasing (algebraically). For the remaining 26 stars D < I, except in the case of η Virginis (bright component), where D = I, corresponding to ω = 180°.*
The apparent grouping of the periastron about certain values of ω is a yet more striking feature, which is clearly shown in the annexed diagram. That such a distribution of the apses really exists is, of course, very improbable--so improbable that we are certainly justified in seeking a different explanation of the observed facts. In other words, the elliptic elements, e and ω, as computed and published for the orbits under notice, are probably illusory ; the "observed radial velocities," upon which they are based, being vitiated by some neglected source of systematic error.†
It now remains to point out the probable nature of this source of error. Two distinct hypotheses are suggested, viz.:
(1) The spectrum-lines, for the stars under notice, are
curve has been found. The elements of U Aquilae and X Sagittarii are as yet
unpublished. In the case of δ Cephei, Belopolsky's value for ω (272°.3) as
printed in the Astrophysical
Journal (February 1895) is erroneous. For the benefit of readers
unversed in this
subject it may be added that P denotes the period of revolution; e the eccentricity;
ω the longitude of periastron, reckoned from the
ascending node; K the "single
amplitude," 2K the total range in the star's
"radial velocity."
* Excluding those stars for which e ₹ 0.10, we find:
D = I for one star,
D > I for two stars,
D < I for 21 stars
D > I for two stars,
D < I for 21 stars
†The period P may of course be relied upon; and it is satisfactory to note that this element has in many cases been determined with a high degree of precison. In cases such as that of Capella, for which the oscillation-curve is almost symmetrical, the computed values of K and a sin i are doubtless nearly correct.
Orbits and Velocity Curves of Spectroscopic Binaries 73
periodically shifted from their normal positions, owing to exceptional conditions
of pressure
or temperature in the star's photosphere, or its surrounding atmosphere.
(2) The disks of the stars under notice are not uniformly bright. The distribution of surface- brightness in longitude is for each star, unequal, and for some stars, distinctly unsymmetrical. Such conditions, combined with rapid axial rotation, would result in a more or less unsymmetrical broadening of the spectral lines. The effective result would be a periodic shift of these lines, as measured on the spectrograms.
The possible source of error referred to in (1) has been made the subject of careful investigation.* In a few cases, such as that of Mira Ceti, there is evidence that a "physical shift" of certain lines in the star-spectrum does actually occur.† On any rational theory, however, it is very unlikely that physical causes would give rise to periodic displacements, affecting in a similar degree the positions of several or many lines (due to various elements) in the spectrum of a star.
The second hypothesis rests upon a much more substantial basis. It was suggested by a perusal of Dr. Albrect's paper on "A Spectrographic Study of the Fourth-Class Variable Stars Y Ophiuchi and T Vulpeculae."‡ In that paper, Dr. Albrecht calls attention to a most important relation which exists between the light and velocity curves of δ Cephei variables. "In every observed case," he remarks, "light- maximum and greatest velocity of approach occur within one-fifteenth of the period of each other. Likewise minimum brightness and greatest velocity of recession occur at the same time."
* Among recent papers dealing with this subject are those of Humphreys ( Astrophysical Journal, 26, 18, 297, 1907), Larmor (Ibid., 26, 120) and Duffield (Ibid., 26, 375). The researches of Julius on "dispersion-bands," should be considered; also the possibility that a shift of the spectral lines may result from electrical or magnetic conditions in the stellar atmosphere.
†See papers by Campbell ( Astrophysical Journal, 9, 31, 1899), Stebbins (Ibid., 18, 341, 1903) and Plaskett (Jour. Roy.Ast. Soc. Can., 1, 45, 1907).
‡Astrophysical Journal, 25, 330, 1907
74 J. Miller Barr
An inspection of the accompanying table will show that it includes eight variables of the
δ Cephei type.* Their orbits, according to the published elements, are more or less
decidedly elliptic--the computed values for the eccentricity e varying from 0.10 in
the case of Y Ophiuchi to 0.489 in that of η Aquilae. If we assume
that these
orbits are in reality nearly circular,† it would appear that the observed facts--as graphically
summarized in the light- and "velocity"-curves--may be explained on the second hypothesis
outlined above. The unsymmetrical distribuiton of light on the discs, as postulated for these
stars, is probably due to tidal action, modified by an unequal angular rotation in different
latitudes, such as exists in the solar photosphere.
Accepting this theory, we must suppose that the preceding side of the revolving star is,
on the whole, more luminous than the opposite hemisphere.‡ A similar state of things seems to
exist in certan variable stars of the Algol type--notably S Cancri, U Coronae, δ Librae.
For such stars, the rise from minimum to maximum brightness is less rapid than the fall from
maximum to minimum. This fact would seem to admit of only one probable explanation, which is
in harmony with our present theory, viz., that the advancing front of such a star, as it
traverses its orbit, is more luminous than the
rear side.§
Further evidence tending in the same direction is afforded by certain facts of observation,
which are here summarized :
*The light curve of one of these stars, viz., W Sagittiarii, is apparently subject to distinct changes in form. According to Schmidt's observations (1866-76) it was formerly of the δ Cephei type; but the Harvard observations of 1898 give a light-curve in which the decrease of light is more rapid than the increase (H. C. O. Annals, 46, Part II).
†This assumption, for theoretical reasons, seems highly probable when the shortness of the periods is considered. (Cf. Darwin and See on the theory of tidal evolution).
‡Cf. Curtiss
(Astrophysical Journal, 20, 186, 1904), Albrecht
(Ibid, 25, 330, 1907),
and Loud (Ibid, 26, 369, 1907).
{For Curtiss, the page number is given as 186. It may be
149,
231 or
232.}
§Strictly speaking, this remark applies only to that hemisphere of the star which is turned towards the earth about the time of minimum brightness.
Orbits and Velocity Curves of Spectroscopic Binaries 75
(a) Distinct irregularities occur in the "velocity-curves" of certain variable stars,
and these correspond with inequalities in the light-curves of the stars.
(b) Broad, unsymmetrical lines have been noted in the spectra of several binaries--
notably δ Orionis.
(c) In the interesting case of η Virginis,* Ichinohe has obtained dissimilar
velocity curves from measures of spectrograms taken, respectively, with full dispersion and with
a single-prism spectrograph. This remark applies to the brighter member of the system. For the
faint component, a double curve having the same period (71.9 days) has been found.
Moreover, the deduced "radial velocity of the center of gravity" is, for the bright component,
-0.4 km., and for the fainter star +30 km. -- a most significant difference.
The further discussion of this interesting subject is reserved for a future paper. In the latter
I
hope to deal with certain details of the theory here advocated.† and to offer some hints
concerning practical methods for the separation of effects due, respectively, to axial rotation
and orbital revolution of the stars under notice.
ST. CATHARINES, ONT.,
February 10, 1908.
{Barr's graph of computed ωs, with the eight Cepheid variables and three stars, with unknown eccentricity and orbit speed removed, can be seen at: barr.htm.}
Related Articles
Pub. Astron. Soc. Pac, 61, 93, 1949
fritzius@bellsouth.net
Top