Home | Up one level | Previous | Next
Table of Contents | Previous Section | Next Section
14. -- STUDY
OF GREAT SPEEDS
WALTER RITZ
Translated (1980) from Recherches critiques sur l'Ėlectrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.
Annales 254 (Oeuvres 408)
The case where the speed of electrons is comparable
to the speed of light is presented only
Annales 255
for β rays of radium. We have studied the deviability of these
rays under the influence of an electrostatic field and under that of a magnetic
field produced by electromagnets, that is neutral closed currents, whose
electrons have speeds v' very small in relation to c. The
accelerations always stay small in these experiments.
We can consequently develop again, in expression (VI) of
the elementary force, the quantities r, u2,
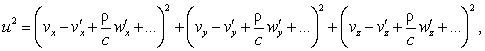
Let v/c=β be a new vector of length comparable to (Oeuvres
409) unity; we will have
(35) 
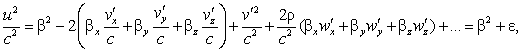
(36) 
(37) 
In
expression (VI) of Fx one can develop φ, ψ
following 
since 
differ from
Annales 256
these values only
by very small quantities ε, η of the order of 
, . . . ,we will have
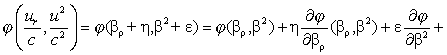
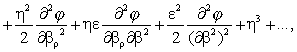
(38) 
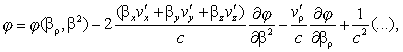
(39) 
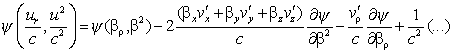
The
expression (VI) of Fx will thus become
(40) 
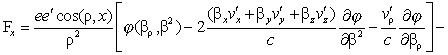
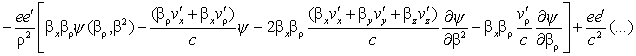(Oeuvres 410) The terms in
1/c2 will be negligible compared to those of the first order; for
the electrostatic action (v'=0) it
will simply become
(41) 
To obtain
the action of an element ds' of a
neutral
Annales 257
closed current whose
electrostatic charge can be neglected, that is for which the positive and
negative charges 
are clearly equal by unity of volume and of
opposite signs, we have only to add the sum of the actions of the positive and
negative ions of ds' on the electron e;
let v1' , v2'
be the speeds of the positive and negative ions, the
conductor or magnet being at rest, we will have
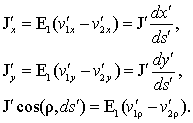
In the sum of the actions of both kinds of ions on e,
the terms independent of v' being taken with opposite signs are canceled
in (40), and there remains
(42) 
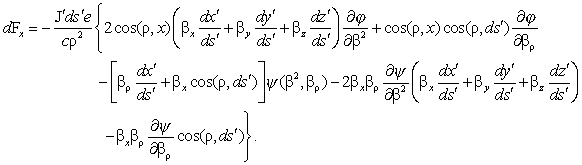
The action of
the current is thus proportional to its intensity. Furthermore, two elements of
parallel current of opposite direction and of the same intensity have no
action. If therefore we consider a uniformly magnetized magnetic sheet as being
a system of very small closed currents of the same intensity, only the parts of
these currents situated on the edge of the sheet will have a noticeable action; (Oeuvres 411) the effect of the currents situated at the interior
will tend towards zero with the dimensions and the distances of the currents.
Such a magnetic sheet will therefore be equivalent
Annales 258
to a closed current circulating on its
contour: this is exactly the reasoning that one makes in electrodynamics, and
it would be easy to give it a more rigorous form.
Similarly, F being a linear function of the cosine
directions 
of the current
element, the principle of the sign currents is satisfied for J.
But there ends the analogy with classical
electrodynamics. Thus for weak speeds (that is to say small β) we saw
earlier that the action Fx, Fy, Fz of a closed
current on a moving electron is perpendicular to the velocity of the latter. It
is not so, in general, for β compared to unity. Indeed,
the component R of F parallel to β will be
(43)
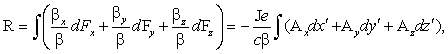
where we put,
to abbreviate
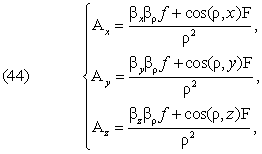
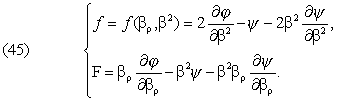
The quantity R will be nil for all
closed circuits only if 
is a total differential, that is we have
Annales 259
(Oeuvres 412) But β2 is independent
of x', y', z' and we have
.
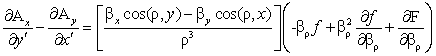The
condition necessary and sufficient in order that the force be perpendicular to
the speed will thus be that the expressions f, F, formed by means of φ, ψ,
satisfy the differential equation
(46) 
For very small β, f is a constant f0
and F is equal to 
; the relation is satisfied.
When φ and ψ do not depend on
βρ, the relation take the simple form f=0.
Likewise, the action of a closed solenoid, or of
a closed electromagnet, is not nil in general, unless a certain
differential equation of the third order between φ and ψ is satisfied.
Finally, more generally, the knowledge of the
magnetic field in a point is not sufficient to determine the force that an
electron in very fast motion will experience at that point, unless the
stated relations are satisfied. This last force is determined only when we give
the disposition of currents (assuming the magnets being replaced by the
equivalent currents) and by this the values of βρ for the
diverse elements of current.
The experiment should thus first of all decide if
the
Annales 260
several laws of electromagnetism just in question apply to the β
rays of radium. Leaving the notion of field, these questions are not even asked
and it is no doubt for this reason that, to my knowledge, no precise
quantitative experiment has yet answered them. Kaufmann’s fine experiments,
undertaken towards a different goal, do not allow answering them, as we are
going to see.
On the whole, the notion of field will apply to the
action that (Oeuvres 413) β rays undergo only under certain conditions; we
have moreover shown that this notion introduces, in general (that is the
forces and the field depending on the speeds), absolute motion. The ordinary
effects of the magnetic field escape this rule only to a certain approximation
(neglecting the motion of the Earth, etc…)
Table of Contents | Previous Section | Next Section
Home | Up one level | Previous | Next
Top