Home | Up One Level | Previous | Next
Table of Contents | Previous Section | Next Section
§13. –HERTZIAN OSCILLATIONS.
WALTER RITZ
Translated from Recherches
critiques sur l'Ėlectrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.
Annales 252
(Oeuvres 406)
While concerning, as in the preceding sections, the hypothesis that the
speeds are small in relation to c, we are going to assume the
acceleration to be very great; such phenomenon will be either of very short
duration or oscillatory. In hertzian oscillations, the speeds, corresponding to
weak currents, will scarcely exceed values on the order of 1 cm per second and
the distance where one may study them may be evaluated to a very small
number
of wavelengths.
The number of oscillations per second varies from 108 (corresponding
to 3 meters of wavelength) to 1011. As to the amplitudes of the
electron [oscillations], they are extremely small, as the speeds remain small
despite the very great frequencies. Under these conditions, the quantity 
is always very small, and the case which has been in question
doesn’t present itself. Indeed, let us suppose the vibrations to be sinusoidal,
and let | v'| be the maximum value of v', | w'r| that of w'r, n the
number of oscillations per second, (Oeuvres 407) mλ the maximum distance where we may observe the
waves, m is scarcely on the
order of 10 to 100. We will have
be
from where
a number, we have
seen, comparable to 10-9 or 10-8.
We have designated by R the vector whose components are x-x', y-y', z-z'. We have
thus
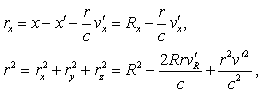
from which
follows
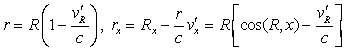
to the terms in
about 
. The first term of (31) is therefore written
.
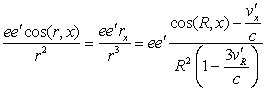This expression is very clearly identical to the first term of (33).
Indeed, in Lorentz’s theory, the center of disturbance remains fixed in
relation to the exciter and to the resonator, when, as we suppose,
the latter are immobile in relation to the ether (the material movements are
besides infinitely slow in relation to the phenomena in question). This center
disturbance therefore coincides with the position of x', y', z' at a certain moment; but the amplitude of the
movements of the electrons being extremely small, the quantities Rx,
Ry, Rz, R are very clearly constant. The
electrostatic terms are therefore obviously identical in both theories.
Besides, the ratios of sizes and direction of r and of R differ
only (Oeuvres
408) in quantities of the order of 
, that is 10-10; one may thus certainly replace r
and R by each other in the second terms of formulas (31) and (33), and
even in the argument 
; this last hypothesis comes back to identify the speeds of
propagation and the phases which are between them in the ratio of 1 to 1+10-10,
that is differing only in a quantity which these experiments can not show.
In summary, both theories lead, for hertzian oscillations, to exactly the
same results.