Home | Up One Level | Previous | Next

Table of Contents | Previous Section | Next Section

§12. – ELECTRIC OSCILLATIONS. GENERAL CONSIDERATIONS.

WALTER RITZ

Translated from Recherches critiques sur l'Ėlectrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13,   p. 145, 1908.

Annales 248 (Oeuvres 403)

      We have seen in the preceding sections, that for very rapid oscillations, only the accelerations are

Annales 249

to be retained besides the electrostatic term, the (effect of the) speeds being negligible compared to them. It will no longer be permitted to refer to developments which we have used up until now, and we must go back to formula (VI), using u=0. It then becomes

(31)    

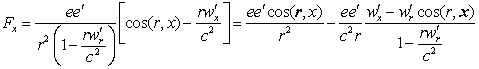
     In Lorentz’s theory, only the electric force will play a role[1]

(32)                            [*]

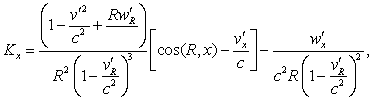(Oeuvres 404) and we can also neglect the terms in so that it (the expression) becomes

(33)                        

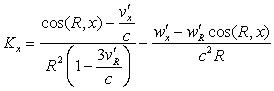
and this is for any value of R which would not be incomparably smaller than 1 cm, and a fortiori (even more so) for large values.

     The second terms of the two formulas (31), (33) correspond to a force perpendicular to the radiation vector,

Annales 250

which in optics (where the term in 1/r² disappears) plays the role of Fresnel’s vector. It depends only on x, y, z, t, and not on v; the notion of field may thus apply, that is to say that we may consider the distribution of this force in space independently of the presence or absence of an electron, which would no longer be the case if it depended on the speed of the latter.

     General discussion. – Formulas (VI) and (31) demand a general remark. They contain, in effect, the factor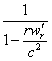, which becomes infinite for sufficiently large values of r. I am going to show that there nevertheless result from these expressions only finite values.

     Let us consider a charge e' vibrating parallel to the x-axis and whose speed v'= v'(t') is nil for t'=0 and afterwards positive. The wave emitted at t'=0 propagates[**] the length of the axis with the speed c, and reaches a fixed point P situated on the positive axis at an instant t>t'>0. Then the speed of propagation increases, and will be c+v' for the wave emitted at . This wave will therefore overtake the previous one at a certain distance x₀, then will pass it. At point x₀ the two waves emanating from e' at t'=0 and  will arrive simultaneously. The speed v' remaining positive, the number of waves arriving simultaneously at x₀ may still increase; but, when v' diminishes or changes sign, this case no longer presents itself. Where the position of P and the movement of e' are given, the time of arrival t is a function f(t') clearly determined from t', given by the law of propagation [analytically by formula  (II^a) (Oeuvres 405) resolved in relation to t]. On the contrary, the function t'=φ(t) may present, for a given value of t, an finite number of distinct determinations as we have just seen. Let us show t'

Annales 251

in ordinates, t in abscissas, and suppose the relative speeds are greatly inferior to c; the curve t'=φ(t) will oscillate from side to side of the straight line , where r₀ is the average distance from e' to P. Parallels to the t-axis will not cross it except at one point; parallels to the t'-axis, at one of several points; among these latter, the tangents to the curve correspond to the points where becomes infinite and where the two values become equal. If  remains finite at this point (that is to say if there is no inflexion), the values of will tend towards great values and of opposite signs.

     These considerations are clearly general and apply even when P is in movement, as soon as the relative speeds become less than c. We have seen [formula (6) obtained by differentiation of (II)] that

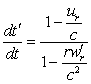
     The denominator therefore annuls itself and changes sign precisely at the instant when two different values  are corresponding to a same instant of reception, and tend to become equal. But it has been specified (§2) that the action of e' on e is the sum of the actions corresponding to Let us multiply and divide F_x (VI) by . This expression will be written

where Φ remains finite and continuous for the instant where and become infinite. The sum of the terms

Annales 252

relative to  and

(34)                                       

(Oeuvres 406) will remain finite², because  and for the critical instant.

------------------------------

²  To rigorously demonstrate this, it is sufficient to see that the differentiation of (II^a) permits us to obtain the development of the function t'=φ(t) in the vicinity of a given point. For the singular point , the known methods give following developments upon , each sign corresponding to one of the two branches which rejoin at τ'. We have

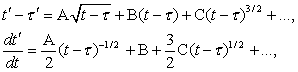
and (34) will be developable as well and will not contain the integer powers of t-τ' ; the fractional powers eliminate themselves.  It will be therefore limited. If

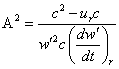
is unlimited in , this reasoning is not applicable any more; but these cases are exceptional, and we have to keep account here of the finite dimension of the electron: the impetus because it remains finite in all these cases.

Translation editor notes:

[*] In expression (32) there needs to be a c^2 in the denominator of the third term inside the first upper parenthesis.

[**] Even though Ritz uses the word propagation, which would seem to imply a wave action impressed on a deformable medium, his mathematical reasoning is more in line with the idea of ballistic projection of his fictitious particles.  (In Lorentzian ether there is only one speed of propagation, i.e., the speed of light.)