Home | Up One Level | Previous | Next
Table of Contents | Previous Section | Next Section
§11. –ACTION OF A RIGID CHARGED BODY ON
ITSELF.
ELECTROMAGNETIC MASS
WALTER RITZ
Translated from Recherches
critiques sur l'Ėlectrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13,
p. 145, 1908.
Annales 246
(Oeuvres 401)
In all that precedes, we have neglected the action of electrons on
themselves; we are going to calculate it supposing the mass equal to M,
the electric densities in two points xyz, x'y'z' being
ε, ε'; furthermore, we will make abstraction of a rotation of the
electron, and consider only a quasi-stationary
translation movement, that is to say where formula (13) for F* remains
applicable. Formula (V) will then give
![]()
The terms in u are nil in the expression of F, since the
speed is the same for all elements of volume; the electrostatic term will again
give zero, because it satisfies the principle of action and reaction; there
remain only the terms relative to accelerations,
and we have
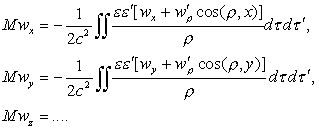
The body will therefore exert on itself a force that is a
linear function of the accelerations, it is to say a reaction of anisotropic
inertia in general (that is to say dependent on the direction (Oeuvres 402) of w in relation to the electron):
(30) 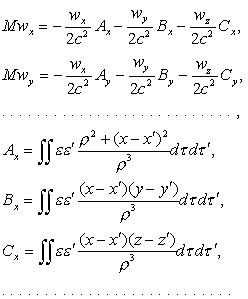
where each
combination of elements dτ, dτ' is taken twice.
These formulas are identical to those that result from Lorentz’s theory[1]
of low speeds; this is a result of the identity of the terms relative to
accelerations in both theories.
When the body presents certain symmetries, this reaction becomes parallel
to w; in this case, the x-axis being parallel to w, the quantity
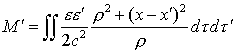
will simply play the role
of electromagnetic mass added to the mass M. Such is therefore the result
of the inequality of the action and reaction in our theory for this particular
case.
Besides, it is evident that this result subsists even at great speeds, as
the terms in u will continue to be identically nil; the electromagnetic
mass will not depend on speed in our theory and Kaufmann’s experiments should
receive a new interpretation. Thus we will not be able to conclude from this
that mass is of electromagnetic origin, but nothing stops us from admitting
this hypothesis, at least for electrons.
Taking into account the terms in 1/c3, we obtain a new (Oeuvres 403) resultant force
![]()
that an electron
of total charge e exerts on itself; we find it again, with the same
coefficient, in Lorentz’s theory[2].
This force, which must be added to the right side of equation (30), does not
depend, as the inertia reaction does, on the form of the body, that is to say
of the electron; it corresponds to a sort of friction determined by the loss of
energy by radiation. In the solution of the equations where the term of the
third order intervenes, it is only permissible to take into consideration the
integrals corresponding to slow phenomena, for which developments in this
series remain valid.
[1] Lorentz, Elektronentheorie, p.190. (Take into
account the difference in units.
[2] Loc. cit.