Home | Up One Level | Previous | Next
Table of Contents | Previous Section | Next Section
PHENOMENA OF SLOW VARIATION
 3. -- GENERAL CALCULATION OF
FORCES
3. -- GENERAL CALCULATION OF
FORCES
WALTER RITZ
Translated from Recherches
critiques sur l'Ėlectrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.
Annales 223
(Oeuvres 382)
We will transform the expression of F
starting from the hypothesis that the developments
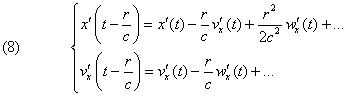
(Oeuvres 383) are very convergent and we want to approximately calculate F up
to terms of third order (in c-3).
Let’s denote by ρ the vector whose components are x(t)-x'(t),
y(t)-y'(t), z(t)-z'(t) , in other words the present distance
between two electrical points, and let Aρ be the component of the
vector A in the direction ρ. We will have then,
according to (2),
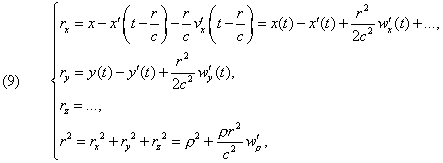
from which finally
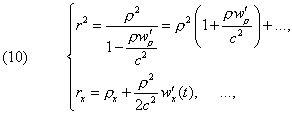
(11) ![]()
Likewise
(12) 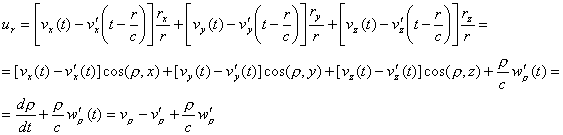
The expressions u2, ur2
entering F only with the factor 1/c2, their expansion
will stop with the first term: u2 will be the square of the
current relative speed of
the two points, that is
![]()
and
![]()
(Oeuvres 384) Neglecting the terms which in the expression
(VI) for F would be multiplied by 1/c3, it finally
comes to
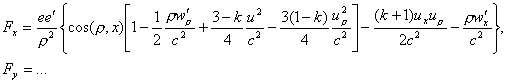
(13) 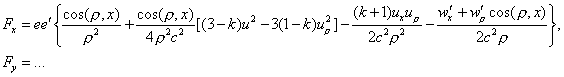
where, let’s say it again, all the magnitudes should be taken at the
moment t. We thus found again the very convenient form of action at a
distance. We can see that the action is not equal to the reaction, but the
difference is a term containing only the accelerations and not the speeds.
This formula can be written
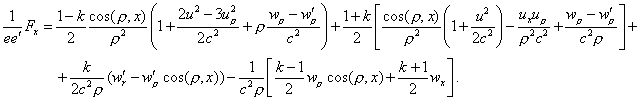
Now 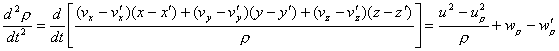
and ![]()
in the manner that the first parenthesis is written , since ![]()
![]() [ = 0? trans. Ed.]
[ = 0? trans. Ed.]
[Need something like “= 0”
for this expression to make sense. Comments welcome]
(Oeuvres 385) as in the well known law of
Weber; the second represents Riemann’s law ([1]),
the third is equal to
![]()
On the whole, concerning the speeds, we are now in the presence of the
most general linear combination of the two laws proposed by Weber and Riemann
for the explanation of electrical phenomena. Yet, we know, and it is easy to
check, that these two formulas can be written in the classical form
![]() ,
,
where 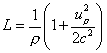 for Weber, and
for Weber, and 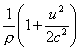 for Riemann.
for Riemann.
Their linear combination will susceptibly be
of the same form, and, in putting
(14) 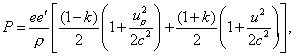
we will have
(15) 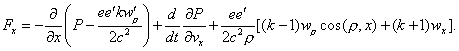
Formulating very special hypotheses about the nature
of the current of conduction, and which today should be considered as
inadmissible, at least for the electrolytes, Weber and Riemann have shown that
their formulas represent well known laws of electrodynamics and of induction in
closed circuits. We will demonstrate that this result is independent of these
special hypotheses ([2])
and it is extended even to actions of closed currents of the free ions of
cathode rays for example, and to actions (Oeuvres 386) that static electricity in
motion exerts on a magnet (in other words, a system of closed currents).
In all the phenomena of this kind observed until now, there is at least one closed
circuit and this is a very important point. As for phenomena of induction in
open circuits, very fast, they depend uniquely on the term containing
the accelerations w'; yet we will see that this term is the same in both
theories: it is entirely determined by the experiments made on the hertzian
oscillations, and we can say that all experimental confirmations of
Maxwell’s and Lorentz’s theory are based only on this term and on the fact of
propagation. As for the manner that these speeds enter the formula of the
elementary force,
we are no more informed about this subject than Weber, Riemann and
Clausius were,
in spite of the experiments on cathode rays, the Rowland effect, etc., etc.
It is interesting to compare this formula to that
resulting from Lorentz’s theory when we develop it up to the terms of 2nd
order. It comes, according to (III)
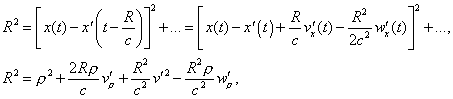
the quantities v', w' being taken for the time t, we
resolve it in relation to R and re-expand it; it will then become
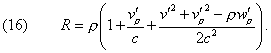
Likewise, to the terms of the order 1/c2
[because, ![]() appearing in (IV)
with the factor 1/c, this approximation is sufficient],
appearing in (IV)
with the factor 1/c, this approximation is sufficient],
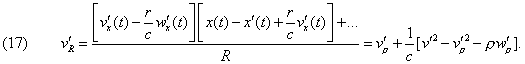
(Oeuvres 387) The expression of potentials Φ, A given
by Messrs. Liénard and Wiechert ([3])
become
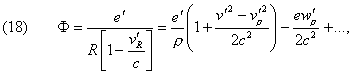
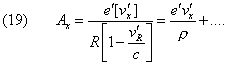
The component ![]() of the force, of
which the general expression for the potentials is
of the force, of
which the general expression for the potentials is
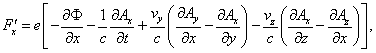
becomes, to the terms of the order 1/c2,
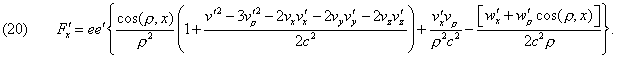
We see that this expression agrees with (13) only
in what concerns the electrostatic term ![]() and the
accelerations. We can put it in the form
and the
accelerations. We can put it in the form
![]()
as Mr. Schwarzschild demonstrated, by setting
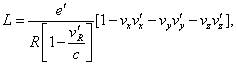
(Oeuvres 388) that is
![]()
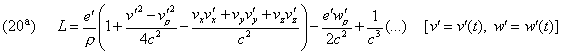
[1] B. Riemann, Schwere; Elektrizität und Magnetismus, Hannover, 1876, paragraphs 98, 99. On this
subject see Enzyklopaedie der Mathematische Wissenschaftem, vol. V, Art.
12, p. 38 and 47 (Reiff and Sommerfeld).
[2] It is what different scientists remarked, at
least concerning particular cases. See Poincaré: Electricité et
Optique, p. 263 (2nd ed.)
[3] Liénard, L’Eclairage
électrique (Electric lighting), vol. XVI, 1898, pp. 5, 53, and 106. Wiechert, Archives
néerlandaises (Netherlands Archives), vol. V, 1990, p. 549. For the case
when the electricity is distributed in a homogenous manner and fixed to solid
in translation, we can use these same formulas, no matter what the distance is,
by replacing e, e' by de, de'; it is what we will see by
developing directly under the sum sign in the general formula of potentials
(formulas (XII) and (XIII) in the 1st part).