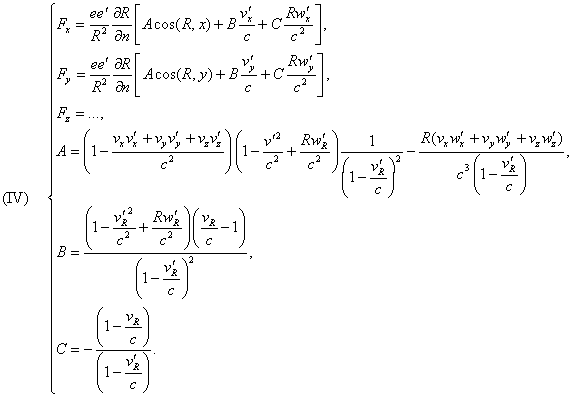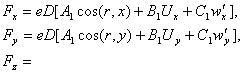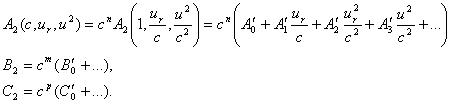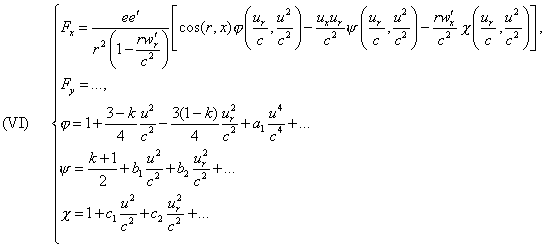Home | Up One Level | Previous | Next

Table of Contents | Previous Section | Next Section

2. – THE ELEMENTARY FORCE

WALTER RITZ

Translated from Recherches critiques sur l'Ėlectrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.

Annales 217 (Oeuvres 377)

      We saw that Lorentz’s theory is expressed, in final analysis, by the statement of an elementary law of action between two charged elements of volume. A mobile corpuscle P’(x’,y’,z’), carrying the charge e’, exerts on another P of charge e placed in xyz a force depending on the speed v of this latter, of  the direction 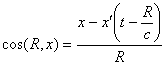, . . . and of the radius R of the wave emitted by P’ at the moment t’= t - R/c, and reaching P at instant t; and finally, of the speed v’ and of the acceleration w’ of P’ in t’. We have (the system of coordinates being at rest in relation to the ether)

,

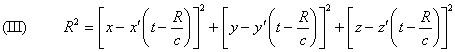the equation which defines R as an implicit function of x, y, z, t when the functions x’=x’(t’), y’,z’ are given. We then conclude

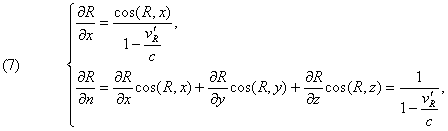
are equations analogous to (4) and (5).

     The elementary force, of which the expression has been given by Schwarzschild [1] for the case of two electrons of

Annales 218

negligible diameter in relation to their distance, possesses a component parallel to R, another parallel to v’, and a third to w’, and (Oeuvres 378) we have

      

 

      The equations of the motions are

the sum being extended to all electrons and more generally, according to the principle of d’Alembert,

     We intend, while keeping the equations (V^a) and (V), to modify the expression of F in a manner as to eliminate the absolute motion. This latter comes to it explicitly

Annales 219

from the absolute speeds v, v’ and implicitly from the law of propagation.

      In the general views expounded previously, the principle of the impossibility of action at a distance will be expressed by the condition that F depends only on the disposition and on the speed of particles around e, in other words, on the vectors U, r and D, as well as the first derivatives of r, D with respect to x, y, z. These derivatives introduce, as we already said, acceleration w’. Also, it (Oeuvres 379) is natural to consider F as proportional to the density D of particles close to e and to the charge e; we can then, exactly as in Lorentz’s formula, decompose F in accordance with the directions r, U, w’ and write 

      The quantities A₁, B₁, C₁, which are independent of the system of coordinates, depend only, by hypothesis, on r, U², U_r. Since  U_x=c cosrx-u_x and U², U_r are expressed linearly by  u², u_r, we can write also   

where A₂, B₂, C₂ are functions of u², u_r; and we will suppose them independent of r. Moreover, for these expressions containing the speeds c, u in an homogenous form, we can write, for the speeds that are relatively small in relation to that of light (n, m, p being exponents carefully chosen)

              

Annales 220

      Although this hypothesis is not indispensable, we will suppose that if we change the sign of the speeds, A₂, B₂, C₂ will not change. In other words, they are even functions of 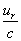; the expansions will not contain odd powers of .

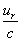     By replacing D with its value from (5), and disposing of some of the coefficients 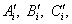 we will finally be able to write F_x in the (Oeuvres 380) form

where k, a_i, b_i, c_i are coefficients remaining arbitrary in the present state of the experience, which also implies that  φ, ψ, χ are almost unknown functions.

      The terms of an order superior to the second play a role only in the pressure of light (which is in the domain of optics, consequently they will not concern us) and in the study of the β rays of radium. It is not surprising, then, that they are not well determined. Yet, we will see that even the terms of the second order, on which the electrodynamic phenomena depend, are not entirely determined by the experiment:  the quantity k remains

Annales 221

arbitrary. The proposed formula is therefore sufficiently general for the goal we are seeking. It is not the most general one, and considerations of the rotary [orbital?]  movements of  electrons would be less general for different reasons.

      The equations of motion will still be (V) and (V^a). In the previously discussed case when waves emitted at different instants by the same electron e’ simultaneously reach the electron e, we will have the sums 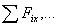to take account each of these actions.

     To show that the new theory effectively takes account of all the facts known in the field of electrodynamics, I will consider first the case where speeds and accelerations are relatively small. It is so, particularly, for all the phenomena belonging to the field of classical electrodynamics, the cathode rays, etc. This case is characterized by
(Oeuvres 381) the fact that we can develop all functions of the form 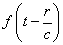 playing a role in it, in very convergent series, proceeding according to the powers of 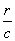, and taking only the first terms. This is what I call slow variation phenomena.

     Secondly, I will consider the case of just about any acceleration with very small speeds in relation to c: this is the case of hertzian oscillations and - up to a certain point - of optics.

     Finally, when speeds are comparable to c, but the accelerations remain small, we are led to Mr. Kaufmann’s experiment on β rays of radium.

     All the electric phenomena observed until now belong to one of these categories.

     We know that the law of the conservation of energy in its classical form W=const is not applicable any more when there is radiation; we must resort to the image of a

Annales 222

 fluid energy or consider the vibratory energy lost by a luminous body or by a hertzian exciter as projected in space with the speed of light and attributing to it a momentum  according to Poincaré’s theorem. From here to the ideas we just expressed there is but one step. But by going into this subject, I would go beyond the purely critical aim I set for myself. I will therefore confine myself to demonstrate that forces, motions and consequently, the work are exactly the same as indicated by Maxwell’s theory, in all the phenomena observed until now; the law of energy, in the measure that it was verified in this domain, is the consequence   

   With the principle of energy, Maupertuis’ principle of least action, which implies the equation of energy in its classical form, ceases to be true in general, likewise the canonical equations and the Hamilton-Jacobi equation of partial derivatives. Nothing lets us believe that Hamilton’s principle will escape from the general rule. In order to be applicable to formula (VI), it would be necessary to introduce in it a term containing the acceleration of e, in other words, an inertial reaction depending on the disposition of external charges. (Oeuvres 382) Weber’s formula contained a term of this sort and Helmholtz [2] demonstrated the inadmissible consequences resulting from it. For an isolated electron, for which 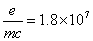approximately, and which is mobile inside an empty charged sphere, everything happens as if the mass were diminished proportionally to the potential of the sphere and were equal to zero for 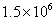 volt (positive) approximately. The acceleration would then become infinite and we can see that the experiment would not be too difficult to execute.

Annales 223

In optics, and for the spectral vibrations where inertial reaction plays an essential role, the influence of electrical charges from the apparatus on the optical properties and the position of rays in the spectrum resulting from the introduction of such a term would be absolutely contrary to the experiment. It is only when Lagrange’s function depends linearly on the speed v of e, as in Lorentz’s theory [3], that these consequences are avoided: but all this demands the introduction of absolute motion. Hamilton’s principle should then be equally transformed when we consider only relative speeds.

     The equations of motion we just wrote are of the second order like those of mechanics, but because of the argument 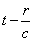, they are, at the same time, functional equations and this very complicated, mixed form cannot be definitive.