|
|
 6. – ACTION AND REACTION 6. – ACTION AND REACTION
WALTER RITZ
Translated (1980) from Recherches critiques sur l'Ėlectrodynamique
Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.
With the ether acting on ions without undergoing action itself, Newton’s principle is
not satisfied by Lorentz’s theory, and Poincaré has shown that we have for the
resultant of translation
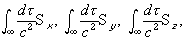
where the integrals are extended over
all space and S is the radiant vector.
Furthermore, an electrified body in uniform motion exerts on itself,
in general, a couple. It is important
to consider separately the diverse aspects of the question which this
poses: can we, from the view-point of the facts, draw from this
inequality of action and reaction an objection to Lorentz’s theory? The answer is affirmative. (Oeuvres 348)
Lets consider, at first, two electrons with charges e,e’,
with coordinates x,y,z; x’,y’,z’, velocities v,v’ and
accelerations
w,w’, placed a great distance apart relative to
their dimensions. Liénard and
Wiechert have shown that for
the potentials produced by e’ we have
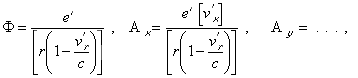
where we have to take the quantities
in brackets at a previous instant t – r/c such that the wave emitted
at this instant reaches (xyz) at t; the vector r is
directed from e’ towards e, and we have the equation
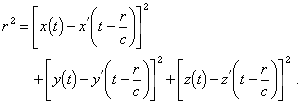
It will suffice to consider the particular case where the velocities
and accelerations are small, so that we can set
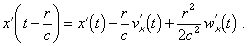
A simple calculation, that we will furthermore find in the Second
Part, leads to the development of θ and A,
from which comes, for the force Fx exerted by e’ on e, the expression
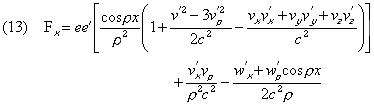
where all the quantities v’, w’, v
must be taken at
the instant t and where r is the actual distance between the points e, e’.
This expression contains velocities and accelerations in a
nonsymmetrical manner that clearly shows the inequality of action and
reaction, even when the accelerations are supposedly negligible and
there is no radiation. In the
(Oeuvres 349) case of uniform translation motion of the points we have
v = v’, w’ = 0;
the term which is multiplied by cos (r,x) is
directed along the line of junction ee’ and satisfies the principle;
the term 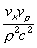 gives a
force parallel to v, applied to e, and another one, equal and
opposite, applied to e’. If
the charges e, e’ were connected by a rigid member, these two
forces would produce a couple whose axis would be perpendicular to the
velocity v and the junction line r. gives a
force parallel to v, applied to e, and another one, equal and
opposite, applied to e’. If
the charges e, e’ were connected by a rigid member, these two
forces would produce a couple whose axis would be perpendicular to the
velocity v and the junction line r.
In the Second Part we will see that no experiment requires this
dissymmetry where the velocities are concerned, and that it is evident a
priori. Since no experiment has
shown anything but relative motions, expression (13) must be replaceable by
another, of the second degree, which contains relative velocities
only. Such an expression,
constrained to be a vector component, wouldn’t present such a dissymmetry.
On the other hand, one experiment by Trouton and Noble, which should have, for the case of
a charged condenser, shown evidence of the couple under question, gave a
negative result. In that it
concerns the terms relative to velocities, the inequality of action and
reaction constitutes therefore a serious objection to Lorentz’s theory.
We can’t say very much, from an experimental point of view
about the nonsymmetrical terms which are dependent on the
acceleration w’. They
contribute, even at small velocities, and when certain conditions of
symmetry are satisfied, to electromagnetic mass and more generally
to a reaction of inertia. For a
uniformly charged sphere, or radius R, the result of elementary actions
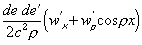
is
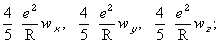
the quantity 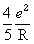 is therefore the electromagnetic mass
and even in (Oeuvres 350) making the same abstraction from*
Kaufmann’s experiments nothing permits denying the possibility of such a
reaction. On the contrary, it is
evident that there’s a considerable advantage, from the point of view of
unifying our concepts, to be able to deduce the reaction of inertia and
kinetic energy from electromagnetic energy.
We will further study the question of the variability of mass as a
function of velocity. is therefore the electromagnetic mass
and even in (Oeuvres 350) making the same abstraction from*
Kaufmann’s experiments nothing permits denying the possibility of such a
reaction. On the contrary, it is
evident that there’s a considerable advantage, from the point of view of
unifying our concepts, to be able to deduce the reaction of inertia and
kinetic energy from electromagnetic energy.
We will further study the question of the variability of mass as a
function of velocity.
*The phrase “en faisant même abstraction” was rendered as “in
excluding” in the 1980 hard copy.
Hertz’s theory satisfies the principle [of action and reaction?] in
a general manner. For example, with the pressure that light exerts on a
body immersed in dielectric air or ether there corresponds a reaction of
the same magnitude applied to these dielectrics, in such a way that, in the first
case, the principle is satisfied by considering the medium only. But experiment has shown the existence of
this pressure, even in the most perfect vacuum. In this latter case there
is no reaction according to Lorentz, but, according to Hertz, there really
is one, and the ether is set into motion.
However, to make this [reaction] perceptible, the ether would have
to quit
concealing itself in all the
experiments. Since it doesn’t
respect this wish, it is difficult to say if, in this case, whether the
logical advantage is on Lorentz’s side, who simply expresses the idea of
action without reaction, or whether it is on Hertz’s side who saves the
principle, but in such a manner that it becomes a simple agreement.
If we are content with the forces exerted by ions on one another
existing without the intervention of an intermediate, such as ether, then
the finite speed of propagation leads to the lack of simultaneity and to
the inequality of actions of ions on one another when they are separated
(generally at least).
In the classical theories of Optics, for example in Sellmeier and
Helmholtz’s dispersion theory, the action of light on molecules is equal to
the reaction of the molecules on the ether. The principle was never
considered as being applicable solely to the material. What we can object to, in the theory, is
that it would be more satisfactory if the intermediate were
devised in such a manner as to explain the matter of the equality of action
and reaction, and I indicated in the Introduction that radiant energy
materializing and projecting at the speed of light constituted such an
(Oeuvres 351) intermediate. We return therefore, in a new form,
to the emission theory, and to use Poincaré’s example, the recoil of an
artillery piece and the force experienced by a body which transmits a wave
of radiant energy in a certain direction are absolutely analogous, which is
not the case when, instead of using this model, we consider energy to be
propagated (the ether theory).
Poincaré has shown that the inequality of action and
reaction doesn’t lead to perpetual
motion in Lorentz’s theory; additionally, under these conditions, we are
obliged to admit the hypothesis of retarded potentials.
|
|