|
|
Table of Contents | Previous Section | Next Section
§17. – GENERAL REMARKS
WALTER RITZ
Translated from Recherches
critiques sur l'Ėlectrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.
Between the new formulas and Lorentz’s theory, there is therefore no
presently known contradiction in the domain of observed facts in
electrodynamics. It is evident that from the viewpoint of mathematical
elegance and simplicity, that the advantage will often be on the side of the
theories of Lorentz; but, on the other hand, the latter can not always avoid
the use of elementary forces. We have even seen that their use is
indispensable in the theory of radiation. In these cases there will be
equivalence. In fact, no deduction may be drawn from Lorentz’s equations
before the demonstration has been done, which are often so complicated, that
the movement of the Earth doesn’t noticeably influence the result; here, the
advantage is on our side.
One of the most fruitful of Maxwell’s
ideas has been the introduction of displacement currents, which form, along
with conduction currents, a system of continuously closed currents to which
Maxwell applied the known laws of electrodynamics (Neumann’s integral, etc.);
it is thus that he arrived at his equations. The preceding developments show
that this application constitutes a second hypothesis: indeed, we have shown
that from our point of view and even from that of Lorentz, that these laws
apply only to neutral currents, and this last point is, for (Oeuvres 423) Ampere’s laws for example, more important than the
other; Maxwell’s hypothesis
Annales 272
comes back to
the introduction of an elementary law for which all experimental basis
is missing.
Our theory necessitates once again the
distinction of open and closed currents. But if one considers not the
mathematical formulas but the physical realities, one finds that the two
orders of phenomena are quantitatively and qualitatively so different that
the practical utility of their synthesis is not perhaps as great as it seemed
at first glance.
The formula for the action of a mobile
electrified point on another, to which Lorentz theory leads, is very
analogous as Schwarzschild(1)
has remarked, to that of Clausius(2), which contains absolute
speeds as well. The latter arrived at this by admitting, among other things,
that there is no action between a galvanic current and an electric charge at
rest. This is very obviously true for neutral currents, as we have seen, but
could be absolutely false in other cases. This hypothesis leads, according to
Clausius as well as Lorentz, to the introduction of absolute movement.
We have seen that, in the expression of
the elementary force, a factor k remains indeterminate. This calls to
mind the analogous result of Helmholtz, and likewise formula (25), which is
applicable to elements of neutral current, is identical to those of
Helmholtz(3) and reduces to that of Ampere for k = -1, and
to that of F. Neumann, Maxwell, and Lorentz for k = +1. The couples
that are added in Helmholtz’s theory are lacking, however, and this point is
essential. Moreover, we now know that only in the case where there is no
radiation does the energy remain constant; the relations that the energy
equation involves between the open current’s inductive actions
___________________________________________________________________________________________
(1) Göttinger Nachrichten, 1903.
(2) Journal für Math.
(Crelle), v.82, 1877, p.85.
(3) Wissenschaft. Abhandl., v.I, p.688, Leipzig, 1882.
Annales 273
and their electrodynamic actions can consequently cease
to be satisfied. This is indeed what happens. For induction
phenomena inside bodies at rest, the equations of Maxwell-Lorentz and
those of Helmholtz(4) become identical if k = 0, as the latter has
remarked. In this (Oeuvres 424) case, only the resistance, the electrostatic
force and the accelerations play a role. Lorentz’s formulas are then identical to ours, which also
correspond to k = 0. As to the consequences relative to stability,
requiring k ≥ 0, they
can only apply to the value of k that figures in induction phenomena
(it is enough, to see it, to suppose the currents effectively nil).
Our formulas therefore always
satisfy, and our parameter k stays entirely undetermined.
It is interesting to notice that, in
bodies at rest, induction phenomena in a closed circuit come only from the
finite propagation speed in our theory. Indeed if we refer to the
developments of section 3, we see that as far as the terms of the second
order are concerned only this finite speed introduces accelerations,
and it is these latter [ones] which determine the induction phenomena, for
the term of the second order 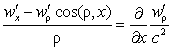 which does not come from these developments gives a
nil electromotive force for a closed circuit. We know that, in the hypothesis
for actions at a distance, the induction phenomena have been deduced from
electrostatic and electrodynamic forces, starting from the energy equation;
in our theory, they are deduced from propagation.
We could determine the k
factor by adopting the theory of metals, proposed by Riecke and Drude,
___________________________________________________________________________________________
(4) Loc. cit.,
p.573, equation (3b).
Annales 274
according to which the speed of electrons in their irregular
molecular movement would be much greater than that of the positive ions, and
which amounts to tens or hundreds kilometers per second. Let
dt' be an element of volume of the metal;
E'dt' be the total charge of the electrons in this
element;
v' be their mean speed.
The body not being
electrified, the action of dt' on a charge e situated in xyz will be by symmetry, considering the irregularities of
the movements, parallel to r, and equation (VI) gives for this
force
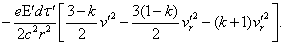
Now we have, on the average
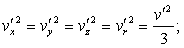
(Oeuvres 425) the force is therefore
(54) 
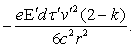
Everything happens as if
the body carried an electric charge 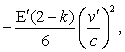 proportional, like v'², to the absolute temperature, and quite considerable; since this
cannot be, it must be that k
is equal to two.
It is true that, if such an action existed, it would no longer be barely possible
to demonstrate, nor doubtless even to admit, Boltzmann’s theory relative to
the distribution of energy between independent coordinates, on which is
founded the hypothesis of large values of v'. If the molecular speeds of positive and negative ions
are, on the contrary, essentially equal, force (54) would cease to exist,
except perhaps for electro-thermal phenomena.
We have seen that the new
theory represents
Annales 275
hertzian oscillations well. The fictitious particles are thus
periodically distributed in time and space. This distribution in turn
provokes the oscillations of other ions or systems of ions; the combination
of these actions by interference, that is to say, by simple superposition,
then gives rise to the diverse phenomena of reflection, refraction,
etc.
When one can consider the
speeds and the amplitude of the accelerations of ions as being infinitely
small, the concordance between Lorentz’s formulas, and mine demonstrated for
hertzian oscillations, continues to exist no matter what the frequency is.
With this restriction, both would represent optical phenomena. But when
the speeds intervene, for example in Fizeau’s experiment on the entrainment
of waves, the agreement ceases; our formulas demand, as do those of Hertz,
total entrainment. I said in the Introduction that one could eliminate the
difficulty by admitting a certain reaction on the part of electric charges
caused by the movement of the [fictitious] particles.
Let us remark in
conclusion, that our law of propagation effortlessly reconciles the
phenomenon of aberration and Michelson’s experiment, which seemed
contradictory in the theory of ether. Indeed, in the second experiment, the
light sources being (Oeuvres 426) drawn along in the Earth’s movement, the speed of their light in
relation to the latter has a different value than that of the speed of light
from the stars, which is independent of the Earth’s movement; the emanative
theory of light which gives such a simple explanation of aberration will
subsist in its essential features.
|
|