Home | Up One Level | Previous | Next
Table of Contents | Previous Section | Next Section
INDUCTION
§9. –THE INDUCTIVE CURRENT IS NEUTRAL
AND CLOSED
WALTER RITZ
Translated from Recherches
critiques sur l'Ėlectrodynamique Générale,
Annales de Chimie et de Physique, Vol. 13, p. 145, 1908.
Annales 242
(Oeuvres 397)
Let ds' be a linear element of one of the closed currents in which
one can decompose the inductive current. Let V' be the speed of the element (which is at the same time that
of the positive ions); we (Oeuvres 398) have
calculated (27) the action of such an element on a mobile ion by supposing V'=0 and neglecting the
accelerations. Let us go back to the calculations without these restrictions,
but also ignoring the electrostatic action of the current, and, a fortiori, all the
terms multiplied by the resultant charge E' of ds, which
comes back to setting 
. Let F be the force exerted by the positive
and negative charges of ds on a unit of charge placed in (xyz),
of speed v. The electromotive force of induction produced in a conductor
wire whose element is ds (dx,dy,dz) is determined by the total
tangential component of F:
In closed
induced currents, we observe only the value of this integral taken along a
closed contour. If therefore F contains terms of the form 
, these terms will give a total differential, and
consequently will disappear from the result.
To calculate F, let us start from formula (15). We can neglect the
term independent of v,
for all closed induced currents. The term containing w
will be multiplied by E', and in consequence will
obviously be nil; thus we will have
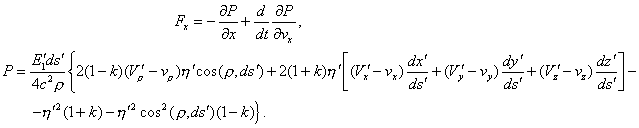
In this expression, the terms independent of v will not figure in
the operation 
, and their partial derivative in relation to x y z alone
intervenes and gives, from that point, a nil result. There will remain
(Oeuvres 399) The first term
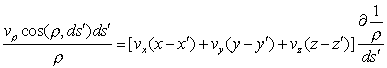
gives, integrated
by parts,
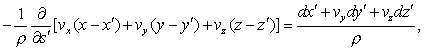
so that we have
in the end
In Lorentz’s theory, there exists a function L given by
(20a) and which leads, by the same operation 
to the expression of the force. The terms in 
of this expression again give zero
for a closed secondary
circuit. The resulting value of L will thus be
Thus the two theories give, for two closed circuits in motion
(for we have made no hypothesis on the movement of the induced circuit, and we
have not supposed v parallel to ds), the same result, in
accord with the experiment.
The more special hypotheses of Weber led, as we know, to the same
results.
Magnets will be treated as in Lorentz’s theory.
One remark is nevertheless necessary. In order for Lorentz’s formula to conform
with
experiment, it is
necessary that only the tangential acceleration 
play a role (in the case of variable currents), the normal
acceleration, proportional to 
being negligible
beside it. Stated otherwise necessary that
must be
essentially reduced to its first term.
(Oeuvres
400) When the secondary circuit
is open, there occur, as we know, potential differences; the study of
several cases where these differences could be observed may easily be treated
by the same methods used up to this point, and I won’t dwell on it.